traces
|
After 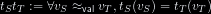
(image error) Size: 1.2 KiB |
|
After 
(image error) Size: 1.4 KiB |
|
After 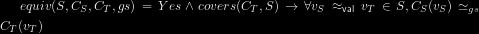
(image error) Size: 3.4 KiB |
|
After 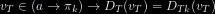
(image error) Size: 1.3 KiB |
|
After 
(image error) Size: 3.5 KiB |
|
After 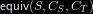
(image error) Size: 965 B |
|
After 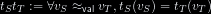
(image error) Size: 1.2 KiB |
|
After 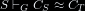
(image error) Size: 787 B |
|
After 
(image error) Size: 1.4 KiB |
|
After 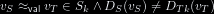
(image error) Size: 1.6 KiB |
|
After 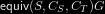
(image error) Size: 1.1 KiB |
|
After 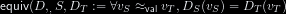
(image error) Size: 1.8 KiB |
|
After 
(image error) Size: 633 B |
|
After 
(image error) Size: 550 B |
|
After 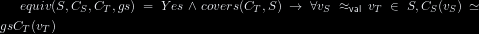
(image error) Size: 3.4 KiB |
|
After 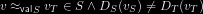
(image error) Size: 1.5 KiB |
|
After 
(image error) Size: 377 B |
|
After 
(image error) Size: 329 B |
|
After 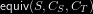
(image error) Size: 965 B |
|
After 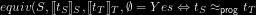
(image error) Size: 1.9 KiB |
|
|
@ -1879,7 +1879,7 @@ for content equality.
|
||||||
{\EquivTEX S \Failure \Failure \emptyqueue}
|
{\EquivTEX S \Failure \Failure \emptyqueue}
|
||||||
\\
|
\\
|
||||||
\infer
|
\infer
|
||||||
{\trel {t_S} {t_T}}
|
{\progrel {t_S} {t_T}}
|
||||||
{\EquivTEX S {\Leaf {t_S}} {\Leaf {t_T}} \emptyqueue}
|
{\EquivTEX S {\Leaf {t_S}} {\Leaf {t_T}} \emptyqueue}
|
||||||
|
|
||||||
\end{mathpar}
|
\end{mathpar}
|
||||||
|
|
@ -1966,24 +1966,24 @@ is empty.
|
||||||
{D_S} {\Guard {e_T} {D_0} {D_1}} {(e_S = b), G}}
|
{D_S} {\Guard {e_T} {D_0} {D_1}} {(e_S = b), G}}
|
||||||
|
|
||||||
\end{mathpar}
|
\end{mathpar}
|
||||||
Our equivalence-checking algorithm $\EquivTEX S {C_S} {C_T} G$ is
|
Our equivalence-checking algorithm is
|
||||||
a exactly decision procedure for the provability of the judgment
|
a exactly decision procedure for the provability of the judgment
|
||||||
$(\EquivTEX S {C_S} {C_T} G)$, defined by the previous inference rules.
|
$\EquivTEX S {C_S} {C_T}$, defined by the previous inference rules.
|
||||||
Running a program tₛ or its translation 〚tₛ〛 against an input vₛ
|
Running a program tₛ or its translation 〚tₛ〛 against an input vₛ
|
||||||
produces as a result /r/ in the following way:
|
produces as a result /r/ in the following way:
|
||||||
| ( 〚tₛ〛ₛ(vₛ) ≡ Cₛ(vₛ) ) → r
|
| ( 〚tₛ〛ₛ(vₛ) ≡ Dₛ(vₛ) ) → r
|
||||||
| tₛ(vₛ) → r
|
| tₛ(vₛ) → r
|
||||||
Likewise
|
Likewise
|
||||||
| ( 〚tₜ〛ₜ(vₜ) ≡ Cₜ(vₜ) ) → r
|
| ( 〚tₜ〛ₜ(vₜ) ≡ Dₜ(vₜ) ) → r
|
||||||
| tₜ(vₜ) → r
|
| tₜ(vₜ) → r
|
||||||
| result r ::= guard list * (Match blackbox \vert{} NoMatch \vert{} Absurd)
|
| result r ::= guard list * (Match blackbox \vert{} NoMatch \vert{} Absurd)
|
||||||
| guard ::= blackbox.
|
| guard ::= blackbox.
|
||||||
Having defined equivalence between two inputs of which one is
|
Having defined equivalence between two inputs of which one is
|
||||||
expressed in the source language and the other in the target language,
|
expressed in the source language and the other in the target language,
|
||||||
vₛ ≃ vₜ, we can define the equivalence between a couple of programs or
|
$\vrel {v_S} {v_T}$, we can define the equivalence between a couple of programs or
|
||||||
a couple of decision trees
|
a couple of decision trees
|
||||||
| tₛ ≃ tₜ := ∀vₛ≃vₜ, tₛ(vₛ) = tₜ(vₜ)
|
| $\progrel {t_S} {t_T} := \forall \vrel {v_S} {v_T}, t_S(v_S) = t_T(v_T)$
|
||||||
| Cₛ ≃ Cₜ := ∀vₛ≃vₜ, Cₛ(vₛ) = Cₜ(vₜ)
|
| $D_S \approx D_T := \forall \vrel {v_S} {v_T}, D_S(v_S) = D_T(v_T)$
|
||||||
The result of the proposed equivalence algorithm is /Yes/ or /No(vₛ,
|
The result of the proposed equivalence algorithm is /Yes/ or /No(vₛ,
|
||||||
vₜ)/. In particular, in the negative case, vₛ and vₜ are a couple of
|
vₜ)/. In particular, in the negative case, vₛ and vₜ are a couple of
|
||||||
possible counter examples for which the decision trees produce a
|
possible counter examples for which the decision trees produce a
|
||||||
|
|
@ -1991,19 +1991,19 @@ different result.
|
||||||
\\
|
\\
|
||||||
In the presence of guards we can say that two results are
|
In the presence of guards we can say that two results are
|
||||||
equivalent modulo the guards queue, written /r₁ ≃gs r₂/, when:
|
equivalent modulo the guards queue, written /r₁ ≃gs r₂/, when:
|
||||||
| (gs₁, r₁) ≃gs (gs₂, r₂) ⇔ (gs₁, r₁) = (gs₂ ++ gs, r₂)
|
| (gs₁, r₁) ≃_{gs} (gs₂, r₂) ⇔ (gs₁, r₁) = (gs₂ +++ gs, r₂)
|
||||||
We say that Cₜ covers the input space /S/, written
|
We say that Dₜ covers the input space /S/, written
|
||||||
/covers(Cₜ, S)/ when every value vₛ∈S is a valid input to the
|
/covers(Dₜ, S)/ when every value vₛ∈S is a valid input to the
|
||||||
decision tree Cₜ. (TODO: rephrase)
|
decision tree Dₜ. (TODO: rephrase)
|
||||||
Given an input space /S/ and a couple of decision trees, where
|
Given an input space /S/ and a couple of decision trees, where
|
||||||
the target decision tree Cₜ covers the input space /S/ we can define equivalence:
|
the target decision tree Dₜ covers the input space /S/ we can define equivalence:
|
||||||
| equiv(S, Cₛ, Cₜ, gs) = Yes ∧ covers(Cₜ, S) → ∀vₛ≃vₜ ∈ S, Cₛ(vₛ) ≃gs Cₜ(vₜ)
|
| $equiv(S, C_S, C_T, gs) = Yes \wedge covers(C_T, S) \to \forall \vrel {v_S} {v_T} \in S, C_S(v_S) \simeq_{gs} C_T(v_T)$
|
||||||
Similarly we say that a couple of decision trees in the presence of
|
Similarly we say that a couple of decision trees in the presence of
|
||||||
an input space /S/ are /not/ equivalent in the following way:
|
an input space /S/ are /not/ equivalent in the following way:
|
||||||
| equiv(S, Cₛ, Cₜ, gs) = No(vₛ,vₜ) ∧ covers(Cₜ, S) → vₛ≃vₜ ∈ S ∧ Cₛ(vₛ) ≠gs Cₜ(vₜ)
|
| $equiv(S, C_S, C_T, gs) = No(v_S, v_T) \wedge covers(C_T, S) \to \vrel {v_S} {v_T} \in S \wedge C_S(v_S) \ne_{gs} C_T(v_T)$
|
||||||
Corollary: For a full input space /S/, that is the universe of the
|
Corollary: For a full input space /S/, that is the universe of the
|
||||||
target program:
|
target program:
|
||||||
| equiv(S, 〚tₛ〛ₛ, 〚tₜ〛ₜ, ∅) = Yes ⇔ tₛ ≃ tₜ
|
| $equiv(S, \llbracket t_S \rrbracket{_S}, \llbracket t_T \rrbracket{_T}, \emptyset) = Yes \Leftrightarrow \progrel {t_S} {t_T}$
|
||||||
|
|
||||||
|
|
||||||
\begin{comment}
|
\begin{comment}
|
||||||
|
|
@ -2012,35 +2012,35 @@ TODO: put ^i∈I where needed
|
||||||
\subsubsection{The trimming lemma}
|
\subsubsection{The trimming lemma}
|
||||||
The trimming lemma allows to reduce the size of a decision tree given
|
The trimming lemma allows to reduce the size of a decision tree given
|
||||||
an accessor /a/ → π relation (TODO: expand)
|
an accessor /a/ → π relation (TODO: expand)
|
||||||
| ∀vₜ ∈ (a→π), Cₜ(vₜ) = C_{t/a→π}(vₜ)
|
| ∀vₜ ∈ (a→π), Dₜ(vₜ) = D_{t/a→π}(vₜ)
|
||||||
We prove this by induction on Cₜ:
|
We prove this by induction on Cₜ:
|
||||||
|
|
||||||
- Cₜ = Leaf_{bb}: when the decision tree is a leaf terminal, the result of trimming on a Leaf is the Leaf itself
|
- Dₜ = Leaf_{bb}: when the decision tree is a leaf terminal, the result of trimming on a Leaf is the Leaf itself
|
||||||
| Leaf_{bb/a→π}(v) = Leaf_{bb}(v)
|
| Leaf_{bb/a→π}(v) = Leaf_{bb}(v)
|
||||||
- The same applies to Failure terminal
|
- The same applies to Failure terminal
|
||||||
| Failure_{/a→π}(v) = Failure(v)
|
| Failure_{/a→π}(v) = Failure(v)
|
||||||
- When Cₜ = Switch(b, (π→Cᵢ)ⁱ)_{/a→π} then we look at the accessor
|
- When Dₜ = Switch(b, (π→Dᵢ)ⁱ)_{/a→π} then we look at the accessor
|
||||||
/a/ of the subtree Cᵢ and we define πᵢ' = πᵢ if a≠b else πᵢ∩π Trimming
|
/a/ of the subtree Dᵢ and we define πᵢ' = πᵢ if a≠b else πᵢ∩π Trimming
|
||||||
a switch node yields the following result:
|
a switch node yields the following result:
|
||||||
| Switch(b, (π→Cᵢ)^{i∈I})_{/a→π} := Switch(b, (π'ᵢ→C_{i/a→π})^{i∈I})
|
| Switch(b, (π→Dᵢ)^{i∈I})_{/a→π} := Switch(b, (π'ᵢ→D_{i/a→π})^{i∈I})
|
||||||
\begin{comment}
|
\begin{comment}
|
||||||
TODO: understand how to properly align lists
|
TODO: understand how to properly align lists
|
||||||
check that every list is aligned
|
check that every list is aligned
|
||||||
\end{comment}
|
\end{comment}
|
||||||
For the trimming lemma we have to prove that running the value vₜ against
|
For the trimming lemma we have to prove that running the value vₜ against
|
||||||
the decision tree Cₜ is the same as running vₜ against the tree
|
the decision tree Dₜ is the same as running vₜ against the tree
|
||||||
C_{trim} that is the result of the trimming operation on Cₜ
|
D_{trim} that is the result of the trimming operation on Dₜ
|
||||||
| Cₜ(vₜ) = C_{trim}(vₜ) = Switch(b, (πᵢ'→C_{i/a→π})^{i∈I})(vₜ)
|
| Dₜ(vₜ) = D_{trim}(vₜ) = Switch(b, (πᵢ'→D_{i/a→π})^{i∈I})(vₜ)
|
||||||
We can reason by first noting that when vₜ∉(b→πᵢ)ⁱ the node must be a Failure node.
|
We can reason by first noting that when vₜ∉(b→πᵢ)ⁱ the node must be a Failure node.
|
||||||
In the case where ∃k \vert{} vₜ∈(b→πₖ) then we can prove that
|
In the case where ∃k \vert{} vₜ∈(b→πₖ) then we can prove that
|
||||||
| C_{k/a→π}(vₜ) = Switch(b, (πᵢ'→C_{i/a→π})^{i∈I})(vₜ)
|
| D_{k/a→π}(vₜ) = Switch(b, (πᵢ'→D_{i/a→π})^{i∈I})(vₜ)
|
||||||
because when a ≠ b then πₖ'= πₖ and this means that vₜ∈πₖ'
|
because when a ≠ b then πₖ'= πₖ and this means that vₜ∈πₖ'
|
||||||
while when a = b then πₖ'=(πₖ∩π) and vₜ∈πₖ' because:
|
while when a = b then πₖ'=(πₖ∩π) and vₜ∈πₖ' because:
|
||||||
- by the hypothesis, vₜ∈π
|
- by the hypothesis, vₜ∈π
|
||||||
- we are in the case where vₜ∈πₖ
|
- we are in the case where vₜ∈πₖ
|
||||||
So vₜ ∈ πₖ' and by induction
|
So vₜ ∈ πₖ' and by induction
|
||||||
| Cₖ(vₜ) = C_{k/a→π}(vₜ)
|
| Dₖ(vₜ) = D_{k/a→π}(vₜ)
|
||||||
We also know that ∀vₜ∈(b→πₖ) → Cₜ(vₜ) = Cₖ(vₜ)
|
We also know that ∀vₜ∈(b→πₖ) → Dₜ(vₜ) = Dₖ(vₜ)
|
||||||
By putting together the last two steps, we have proven the trimming
|
By putting together the last two steps, we have proven the trimming
|
||||||
lemma.
|
lemma.
|
||||||
|
|
||||||
|
|
@ -2056,21 +2056,21 @@ Covering lemma:
|
||||||
|
|
||||||
\subsubsection{Equivalence checking}
|
\subsubsection{Equivalence checking}
|
||||||
The equivalence checking algorithm takes as parameters an input space
|
The equivalence checking algorithm takes as parameters an input space
|
||||||
/S/, a source decision tree /Cₛ/ and a target decision tree /Cₜ/:
|
/S/, a source decision tree /Dₛ/ and a target decision tree /Dₜ/:
|
||||||
| equiv(S, Cₛ, Cₜ) → Yes \vert{} No(vₛ, vₜ)
|
| equiv(S, Dₛ, Dₜ) → Yes \vert{} No(vₛ, vₜ)
|
||||||
\\
|
\\
|
||||||
When the algorithm returns Yes and the input space is covered by /Cₛ/
|
When the algorithm returns Yes and the input space is covered by /Dₛ/
|
||||||
we can say that the couple of decision trees are the same for
|
we can say that the couple of decision trees are the same for
|
||||||
every couple of source value /vₛ/ and target value /vₜ/ that are equivalent.
|
every couple of source value /vₛ/ and target value /vₜ/ that are equivalent.
|
||||||
\begin{comment}
|
\begin{comment}
|
||||||
Define "covered"
|
Define "covered"
|
||||||
Is it correct to say the same? How to correctly distinguish in words ≃ and = ?
|
Is it correct to say the same? How to correctly distinguish in words ≃ and = ?
|
||||||
\end{comment}
|
\end{comment}
|
||||||
| equiv(S, Cₛ, Cₜ) = Yes and cover(Cₜ, S) → ∀ vₛ ≃ vₜ∈S ∧ Cₛ(vₛ) = Cₜ(vₜ)
|
| equiv(S, Dₛ, Dₜ) = Yes and cover(Dₜ, S) → ∀ vₛ ≃ vₜ∈S ∧ Dₛ(vₛ) = Dₜ(vₜ)
|
||||||
In the case where the algorithm returns No we have at least a couple
|
In the case where the algorithm returns No we have at least a couple
|
||||||
of counter example values vₛ and vₜ for which the two decision trees
|
of counter example values vₛ and vₜ for which the two decision trees
|
||||||
outputs a different result.
|
outputs a different result.
|
||||||
| equiv(S, Cₛ, Cₜ) = No(vₛ,vₜ) and cover(Cₜ, S) → ∀ vₛ ≃ vₜ∈S ∧ Cₛ(vₛ) ≠ Cₜ(vₜ)
|
| equiv(S, Dₛ, Cₜ) = No(vₛ,vₜ) and cover(Dₜ, S) → ∀ vₛ ≃ vₜ∈S ∧ Dₛ(vₛ) ≠ Dₜ(vₜ)
|
||||||
We define the following
|
We define the following
|
||||||
| Forall(Yes) = Yes
|
| Forall(Yes) = Yes
|
||||||
| Forall(Yes::l) = Forall(l)
|
| Forall(Yes::l) = Forall(l)
|
||||||
|
|
@ -2092,9 +2092,9 @@ I start numbering from zero to leave the numbers as they were on the blackboard,
|
||||||
I think the unreachable case should go at the end.
|
I think the unreachable case should go at the end.
|
||||||
\end{comment}
|
\end{comment}
|
||||||
0. in case of unreachable:
|
0. in case of unreachable:
|
||||||
| Cₛ(vₛ) = Absurd(Unreachable) ≠ Cₜ(vₜ) ∀vₛ,vₜ
|
| Dₛ(vₛ) = Absurd(Unreachable) ≠ Dₜ(vₜ) ∀vₛ,vₜ
|
||||||
1. In the case of an empty input space
|
1. In the case of an empty input space
|
||||||
| equiv(∅, Cₛ, Cₜ) := Yes
|
| equiv(∅, Dₛ, Dₜ) := Yes
|
||||||
and that is trivial to prove because there is no pair of values (vₛ, vₜ) that could be
|
and that is trivial to prove because there is no pair of values (vₛ, vₜ) that could be
|
||||||
tested against the decision trees.
|
tested against the decision trees.
|
||||||
In the other subcases S is always non-empty.
|
In the other subcases S is always non-empty.
|
||||||
|
|
@ -2102,48 +2102,46 @@ I think the unreachable case should go at the end.
|
||||||
|equiv(S, Failure, Failure) := Yes
|
|equiv(S, Failure, Failure) := Yes
|
||||||
Given that ∀v, Failure(v) = Failure, the statement holds.
|
Given that ∀v, Failure(v) = Failure, the statement holds.
|
||||||
3. When we have a Leaf or a Failure at the left side:
|
3. When we have a Leaf or a Failure at the left side:
|
||||||
| equiv(S, Failure as Cₛ, Switch(a, (πᵢ → Cₜᵢ)^{i∈I})) := Forall(equiv( S∩a→π(kᵢ)), Cₛ, Cₜᵢ)^{i∈I})
|
| equiv(S, Failure as Dₛ, Switch(a, (πᵢ → Dₜᵢ)^{i∈I})) := Forall(equiv( S∩a→π(kᵢ)), Dₛ, Dₜᵢ)^{i∈I})
|
||||||
| equiv(S, Leaf bbₛ as Cₛ, Switch(a, (πᵢ → Cₜᵢ)^{i∈I})) := Forall(equiv( S∩a→π(kᵢ)), Cₛ, Cₜᵢ)^{i∈I})
|
| equiv(S, Leaf bbₛ as Dₛ, Switch(a, (πᵢ → Dₜᵢ)^{i∈I})) := Forall(equiv( S∩a→π(kᵢ)), Dₛ, Dₜᵢ)^{i∈I})
|
||||||
Our algorithm either returns Yes for every sub-input space Sᵢ := S∩(a→π(kᵢ)) and
|
Our algorithm either returns Yes for every sub-input space Sᵢ := S∩(a→π(kᵢ)) and
|
||||||
subtree Cₜᵢ
|
subtree Cₜᵢ
|
||||||
| equiv(Sᵢ, Cₛ, Cₜᵢ) = Yes ∀i
|
| equiv(Sᵢ, Dₛ, Dₜᵢ) = Yes ∀i
|
||||||
or we have a counter example vₛ, vₜ for which
|
or we have a counter example v_S, v_T for which
|
||||||
| vₛ≃vₜ∈Sₖ ∧ cₛ(vₛ) ≠ Cₜₖ(vₜ)
|
| $\vrel {v_S} {v_T \in S_k} \wedge D_S(v_S) \ne D_{Tk}(v_T)$
|
||||||
then because
|
then because $v_T \in (a \to \pi_k) \to D_T(v_T) = D_{Tk}(v_T)$ and $\vrel v_S {v_T \in S} \wedge D_S(v_S) \ne D_T(v_T)$ we can say that
|
||||||
| vₜ∈(a→πₖ) → Cₜ(vₜ) = Cₜₖ(vₜ) ,
|
|
||||||
| vₛ≃vₜ∈S ∧ Cₛ(vₛ)≠Cₜ(vₜ)
|
|
||||||
we can say that
|
|
||||||
| equiv(Sᵢ, Cₛ, Cₜᵢ) = No(vₛ, vₜ) for some minimal k∈I
|
| equiv(Sᵢ, Cₛ, Cₜᵢ) = No(vₛ, vₜ) for some minimal k∈I
|
||||||
4. When we have a Switch on the right we define π_{fallback} as the domain of
|
4. When we have a Switch on the right we define π_{fallback} as the domain of
|
||||||
values not covered but the union of the constructors kᵢ
|
values not covered but the union of the constructors kᵢ
|
||||||
| $\pi_{fallback} = \neg\bigcup\limits_{i\in I}\pi(k_i)$
|
| $\pi_{fallback} = \neg\bigcup\limits_{i\in I}\pi(k_i)$
|
||||||
Our algorithm proceeds by trimming
|
Our algorithm proceeds by trimming
|
||||||
| equiv(S, Switch(a, (kᵢ → Cₛᵢ)^{i∈I}, C_{sf}), Cₜ) :=
|
| equiv(S, Switch(a, (kᵢ → Dₛᵢ)^{i∈I}, D_{sf}), Dₜ) :=
|
||||||
| Forall(equiv( S∩(a→π(kᵢ)^{i∈I}), Cₛᵢ, C_{t/a→π(kᵢ)})^{i∈I} +++ equiv(S∩(a→πₙ), Cₛ, C_{a→π_{fallback}}))
|
| Forall(equiv( S∩(a→π(kᵢ)^{i∈I}), Dₛᵢ, D_{t/a→π(kᵢ)})^{i∈I} +++ equiv(S∩(a→πₙ), Dₛ, D_{a→π_{fallback}}))
|
||||||
The statement still holds and we show this by first analyzing the
|
The statement still holds and we show this by first analyzing the
|
||||||
/Yes/ case:
|
/Yes/ case:
|
||||||
| Forall(equiv( S∩(a→π(kᵢ)^{i∈I}), Cₛᵢ, C_{t/a→π(kᵢ)})^{i∈I} = Yes
|
| Forall(equiv( S∩(a→π(kᵢ)^{i∈I}), Dₛᵢ, D_{t/a→π(kᵢ)})^{i∈I} = Yes
|
||||||
The constructor k is either included in the set of constructors kᵢ:
|
The constructor k is either included in the set of constructors kᵢ:
|
||||||
| k \vert k∈(kᵢ)ⁱ ∧ Cₛ(vₛ) = Cₛᵢ(vₛ)
|
| k \vert k∈(kᵢ)ⁱ ∧ Dₛ(vₛ) = Dₛᵢ(vₛ)
|
||||||
We also know that
|
We also know that
|
||||||
| (1) Cₛᵢ(vₛ) = C_{t/a→πᵢ}(vₜ)
|
| (1) Dₛᵢ(vₛ) = D_{t/a→πᵢ}(vₜ)
|
||||||
| (2) C_{T/a→πᵢ}(vₜ) = Cₜ(vₜ)
|
| (2) D_{T/a→πᵢ}(vₜ) = Dₜ(vₜ)
|
||||||
(1) is true by induction and (2) is a consequence of the trimming lemma.
|
(1) is true by induction and (2) is a consequence of the trimming lemma.
|
||||||
Putting everything together:
|
Putting everything together:
|
||||||
| Cₛ(vₛ) = Cₛᵢ(vₛ) = C_{T/a→πᵢ}(vₜ) = Cₜ(vₜ)
|
| Dₛ(vₛ) = Dₛᵢ(vₛ) = D_{T/a→πᵢ}(vₜ) = Dₜ(vₜ)
|
||||||
|
|
||||||
When the k∉(kᵢ)ⁱ [TODO]
|
When the k∉(kᵢ)ⁱ [TODO]
|
||||||
|
|
||||||
The auxiliary Forall function returns /No(vₛ, vₜ)/ when, for a minimum k,
|
The auxiliary Forall function returns /No(vₛ, vₜ)/ when, for a minimum k,
|
||||||
| equiv(Sₖ, Cₛₖ, C_{T/a→πₖ} = No(vₛ, vₜ)
|
| equiv(Sₖ, Dₛₖ, D_{T/a→πₖ} = No(vₛ, vₜ)
|
||||||
Then we can say that
|
Then we can say that
|
||||||
| Cₛₖ(vₛ) ≠ C_{t/a→πₖ}(vₜ)
|
| Dₛₖ(vₛ) ≠ D_{t/a→πₖ}(vₜ)
|
||||||
that is enough for proving that
|
that is enough for proving that
|
||||||
| Cₛₖ(vₛ) ≠ (C_{t/a→πₖ}(vₜ) = Cₜ(vₜ))
|
| Dₛₖ(vₛ) ≠ (D_{t/a→πₖ}(vₜ) = Dₜ(vₜ))
|
||||||
|
|
||||||
* Examples
|
* Examples
|
||||||
In this section we discuss some examples given as input and output of
|
In this section we discuss some examples given as input and output of
|
||||||
the prototype tool.
|
the prototype tool. Source and target files are taken from the
|
||||||
|
internship git repository\cite{internship}.
|
||||||
|
|
||||||
;; include_file example0.ml
|
;; include_file example0.ml
|
||||||
We can see from this first source file the usage of the /observe/
|
We can see from this first source file the usage of the /observe/
|
||||||
|
|
@ -2154,6 +2152,23 @@ The prototype tool states that the compilation was successful and the
|
||||||
two programs are equivalent.
|
two programs are equivalent.
|
||||||
;; include_file example0.trace
|
;; include_file example0.trace
|
||||||
|
|
||||||
|
The following example shows how the prototype handles ADT.
|
||||||
|
;; include_file example3.ml
|
||||||
|
;; include_file example3.lambda
|
||||||
|
;; include_file example3.trace
|
||||||
|
This trivial pattern matching code shows how guards are handled.
|
||||||
|
;; include_file guards2.ml
|
||||||
|
;; include_file guards2.lambda
|
||||||
|
;; include_file guards2.trace
|
||||||
|
The following source code shows the usage of the OCaml refutation
|
||||||
|
clause.
|
||||||
|
;; include_file example9.ml
|
||||||
|
;; include_file example9.lambda
|
||||||
|
;; include_file example9.trace
|
||||||
|
In this example the tool correctly handles /Failure/ nodes on both decision trees.
|
||||||
|
;; include_file example9bis.ml
|
||||||
|
;; include_file example9bis.lambda
|
||||||
|
;; include_file example9bis.trace
|
||||||
|
|
||||||
\begin{thebibliography}{9}
|
\begin{thebibliography}{9}
|
||||||
\bibitem{cpp_pat}
|
\bibitem{cpp_pat}
|
||||||
|
|
@ -2240,4 +2255,8 @@ https://github.com/janestreet/ocaml-compiler-libs
|
||||||
\bibitem{menhir}
|
\bibitem{menhir}
|
||||||
Régis-Gianas, François Pottier Yann.
|
Régis-Gianas, François Pottier Yann.
|
||||||
\textit{Menhir Reference Manual}.
|
\textit{Menhir Reference Manual}.
|
||||||
|
|
||||||
|
\bibitem{internship}
|
||||||
|
https://github.com/FraMecca/inria-internship
|
||||||
|
|
||||||
\end{thebibliography}
|
\end{thebibliography}
|
||||||
|
|
|
||||||
|
|
@ -1,4 +1,4 @@
|
||||||
Target program constraint tree
|
Target program decision tree
|
||||||
Switch ({ var=AcAdd(-2 AcRoot=param/82); dom=Int [-inf; -1] [3; +inf] v Tag _; }) =
|
Switch ({ var=AcAdd(-2 AcRoot=param/82); dom=Int [-inf; -1] [3; +inf] v Tag _; }) =
|
||||||
Leaf=VConstant:5
|
Leaf=VConstant:5
|
||||||
Switch ({ var=AcAdd(-2 AcRoot=param/82); dom=Int [0; 2]; }) =
|
Switch ({ var=AcAdd(-2 AcRoot=param/82); dom=Int [0; 2]; }) =
|
||||||
|
|
@ -12,7 +12,7 @@ Switch ({ var=AcAdd(-2 AcRoot=param/82); dom=Int [0; 2]; }) =
|
||||||
Fallback=None
|
Fallback=None
|
||||||
|
|
||||||
|
|
||||||
Source program constraint tree
|
Source program decision tree
|
||||||
Switch AcRoot:{
|
Switch AcRoot:{
|
||||||
Int 3 ->
|
Int 3 ->
|
||||||
Leaf='Int 3 '
|
Leaf='Int 3 '
|
||||||
|
|
|
||||||
18
tesi/traces/example3.lambda
Normal file
|
|
@ -0,0 +1,18 @@
|
||||||
|
(setglobal Example3!
|
||||||
|
(let
|
||||||
|
(a/85 =
|
||||||
|
(function t/86
|
||||||
|
(switch* t/86
|
||||||
|
case int 0: (observe 3)
|
||||||
|
case tag 0:
|
||||||
|
(let (*match*/90 =a (field 0 t/86))
|
||||||
|
(catch
|
||||||
|
(if (!= *match*/90 1)
|
||||||
|
(if (!= *match*/90 2) (exit 1) (apply (observe 1) 2))
|
||||||
|
(apply (observe 1) 1))
|
||||||
|
with (1) (apply (observe 1) 0a)))
|
||||||
|
case tag 1:
|
||||||
|
(let (*match*/91 =a (field 0 t/86))
|
||||||
|
(if (!= *match*/91 0) (apply (observe 2) 1a)
|
||||||
|
(apply (observe 2) 0a))))))
|
||||||
|
(makeblock 0 a/85)))
|
||||||
11
tesi/traces/example3.ml
Normal file
|
|
@ -0,0 +1,11 @@
|
||||||
|
external observe : 'a -> 'b = "observe"
|
||||||
|
|
||||||
|
type t = K1 of int | K2 of bool | K3
|
||||||
|
|
||||||
|
let a = fun t -> match t with
|
||||||
|
| K1 1 -> observe 1 1
|
||||||
|
| K1 2 -> observe 1 2
|
||||||
|
| K1 _ -> observe 1 ()
|
||||||
|
| K2 true -> observe 2 true
|
||||||
|
| K2 false -> observe 2 false
|
||||||
|
| K3 -> observe 3
|
||||||
46
tesi/traces/example3.trace
Normal file
|
|
@ -0,0 +1,46 @@
|
||||||
|
Target program decision tree
|
||||||
|
Switch ({ var=AcRoot=t/86; dom=Int 0; }) =
|
||||||
|
Leaf=VConstant:3
|
||||||
|
Switch ({ var=AcRoot=t/86; dom=Tag 0; }) =
|
||||||
|
Switch ({ var=AcField(0 AcRoot=t/86); dom=Int [-inf; 0] [2; +inf] v Tag _; }) =
|
||||||
|
Switch ({ var=AcField(0 AcRoot=t/86); dom=Int [-inf; 1] [3; +inf] v Tag _; }) =
|
||||||
|
Leaf=VConstant:1, VConstant:0
|
||||||
|
Switch ({ var=AcField(0 AcRoot=t/86); dom=Int 2; }) =
|
||||||
|
Leaf=VConstant:1, VConstant:2
|
||||||
|
Fallback=None
|
||||||
|
Switch ({ var=AcField(0 AcRoot=t/86); dom=Int 1; }) =
|
||||||
|
Leaf=VConstant:1, VConstant:1
|
||||||
|
Fallback=None
|
||||||
|
Switch ({ var=AcRoot=t/86; dom=Tag 1; }) =
|
||||||
|
Switch ({ var=AcField(0 AcRoot=t/86); dom=Int [-inf; -1] [1; +inf] v Tag _; }) =
|
||||||
|
Leaf=VConstant:2, VConstant:1
|
||||||
|
Switch ({ var=AcField(0 AcRoot=t/86); dom=Int 0; }) =
|
||||||
|
Leaf=VConstant:2, VConstant:0
|
||||||
|
Fallback=None
|
||||||
|
Fallback=None
|
||||||
|
|
||||||
|
Source program decision tree
|
||||||
|
Switch AcRoot:{
|
||||||
|
Variant K2 ->
|
||||||
|
Switch AcRoot.0:{
|
||||||
|
Bool false ->
|
||||||
|
Leaf='Int 2 Bool false '
|
||||||
|
|
||||||
|
Bool true ->
|
||||||
|
Leaf='Int 2 Bool true '
|
||||||
|
} Fallback: Unreachable
|
||||||
|
|
||||||
|
Variant K1 ->
|
||||||
|
Switch AcRoot.0:{
|
||||||
|
Int 2 ->
|
||||||
|
Leaf='Int 1 Int 2 '
|
||||||
|
|
||||||
|
Int 1 ->
|
||||||
|
Leaf='Int 1 Int 1 '
|
||||||
|
} Fallback: Leaf='Int 1 Unit '
|
||||||
|
|
||||||
|
Variant K3 ->
|
||||||
|
Leaf='Int 3 '
|
||||||
|
} Fallback: Unreachable
|
||||||
|
|
||||||
|
The two programs are equivalent.
|
||||||
70
tesi/traces/example6.lambda
Normal file
|
|
@ -0,0 +1,70 @@
|
||||||
|
(setglobal Example6!
|
||||||
|
(let
|
||||||
|
(mm/81 =
|
||||||
|
(function x/89
|
||||||
|
(catch
|
||||||
|
(if x/89
|
||||||
|
(let (*match*/92 =a (field 0 x/89))
|
||||||
|
(if *match*/92
|
||||||
|
(let
|
||||||
|
(x/83 =a (field 0 *match*/92)
|
||||||
|
x/86 =a (field 0 x/83)
|
||||||
|
*match*/93 =a (field 0 x/86))
|
||||||
|
(catch
|
||||||
|
(if (!= *match*/93 1) (exit 2)
|
||||||
|
(let (*match*/94 =a (field 1 x/86))
|
||||||
|
(if (!= *match*/94 2) (exit 2)
|
||||||
|
(let (x/82 =a (field 1 x/83))
|
||||||
|
(catch
|
||||||
|
(if (!= x/82 2) (exit 3)
|
||||||
|
(let (*match*/95 =a (field 1 *match*/92))
|
||||||
|
(if *match*/95 (exit 1)
|
||||||
|
(let (*match*/96 =a (field 1 x/89))
|
||||||
|
(catch
|
||||||
|
(if *match*/96 (exit 4)
|
||||||
|
(observe
|
||||||
|
[0: [0: [0: [0: 1 2] 2] 0a] 0a]))
|
||||||
|
with (4)
|
||||||
|
(observe [0: [0: [0: 1 2] 2] 0a]))))))
|
||||||
|
with (3)
|
||||||
|
(let (*match*/97 =a (field 1 *match*/92))
|
||||||
|
(if *match*/97 (exit 1)
|
||||||
|
(let (*match*/98 =a (field 1 x/89))
|
||||||
|
(observe
|
||||||
|
(makeblock 0
|
||||||
|
(makeblock 0 (*,int) [0: 1 2] x/82)
|
||||||
|
0a))))))))))
|
||||||
|
with (2)
|
||||||
|
(let (*match*/100 =a (field 1 *match*/92))
|
||||||
|
(if *match*/100 (exit 1)
|
||||||
|
(let
|
||||||
|
(z/88 =a (field 1 x/89)
|
||||||
|
y/87 =a (field 1 x/83)
|
||||||
|
*match*/99 =a (field 1 x/86))
|
||||||
|
(catch
|
||||||
|
(if z/88
|
||||||
|
(let (*match*/101 =a (field 0 z/88))
|
||||||
|
(if *match*/101
|
||||||
|
(let
|
||||||
|
(*match*/102 =a (field 1 *match*/101))
|
||||||
|
(if *match*/102 (exit 5)
|
||||||
|
(let (*match*/103 =a (field 1 z/88))
|
||||||
|
(if *match*/103 (exit 5)
|
||||||
|
(let
|
||||||
|
(x/84 =a x/83
|
||||||
|
y/85 =a (field 0 *match*/101))
|
||||||
|
(observe
|
||||||
|
(makeblock 0
|
||||||
|
(makeblock 0 x/84 y/85) 0a)))))))
|
||||||
|
(exit 5)))
|
||||||
|
(observe (makeblock 0 x/83 0a)))
|
||||||
|
with (5)
|
||||||
|
(observe
|
||||||
|
(makeblock 0
|
||||||
|
(makeblock 0 (makeblock 0 (*,int) x/86 y/87)
|
||||||
|
z/88)
|
||||||
|
0a))))))))
|
||||||
|
(exit 1)))
|
||||||
|
(exit 1))
|
||||||
|
with (1) (observe x/89))))
|
||||||
|
(makeblock 0 mm/81)))
|
||||||
11
tesi/traces/example6.ml
Normal file
|
|
@ -0,0 +1,11 @@
|
||||||
|
[@@@warning "-20"]
|
||||||
|
external observe : 'a -> 'b = "observe"
|
||||||
|
|
||||||
|
let mm = function
|
||||||
|
| [(1, 2), 2]::[] -> observe ([(1, 2), 2]::[])
|
||||||
|
| [(1, 2), 2]::_ -> observe [(1, 2), 2]
|
||||||
|
| [(1, 2), x]::_ -> observe [(1, 2), x]
|
||||||
|
| [x]::[] -> observe [x]
|
||||||
|
| [x]::[y]::[] -> observe [x, y]
|
||||||
|
| [x, y]::z -> observe [(x, y), z]
|
||||||
|
| x -> observe x
|
||||||
5
tesi/traces/example9.lambda
Normal file
|
|
@ -0,0 +1,5 @@
|
||||||
|
(setglobal Example9!
|
||||||
|
(let
|
||||||
|
(test/81 =
|
||||||
|
(function param/82 (if (!= param/82 0) (observe 0) (observe 1))))
|
||||||
|
(makeblock 0 test/81)))
|
||||||
9
tesi/traces/example9.ml
Normal file
|
|
@ -0,0 +1,9 @@
|
||||||
|
[@@@warning "-20"]
|
||||||
|
external observe : 'a -> 'b = "observe"
|
||||||
|
|
||||||
|
let test = function
|
||||||
|
| true -> observe 0
|
||||||
|
| false -> observe 1
|
||||||
|
| _ -> .
|
||||||
|
(* Unreachable; if this annotation was incorrect,
|
||||||
|
the OCaml compiler would error at pattern-checking-time *)
|
||||||
18
tesi/traces/example9.trace
Normal file
|
|
@ -0,0 +1,18 @@
|
||||||
|
Target program decision tree
|
||||||
|
Switch ({ var=AcRoot=param/82; dom=Int [-inf; -1] [1; +inf] v Tag _; }) =
|
||||||
|
Leaf=VConstant:0
|
||||||
|
Switch ({ var=AcRoot=param/82; dom=Int 0; }) =
|
||||||
|
Leaf=VConstant:1
|
||||||
|
Fallback=None
|
||||||
|
|
||||||
|
|
||||||
|
Source program decision tree
|
||||||
|
Switch AcRoot:{
|
||||||
|
Bool false ->
|
||||||
|
Leaf='Int 1 '
|
||||||
|
|
||||||
|
Bool true ->
|
||||||
|
Leaf='Int 0 '
|
||||||
|
} Fallback: Unreachable
|
||||||
|
|
||||||
|
The two programs are equivalent.
|
||||||
9
tesi/traces/example9bis.lambda
Normal file
|
|
@ -0,0 +1,9 @@
|
||||||
|
(setglobal Example9bis!
|
||||||
|
(let
|
||||||
|
(test/81 =
|
||||||
|
(function param/82
|
||||||
|
(catch (if (!= param/82 0) (observe 0) (exit 1)) with (1)
|
||||||
|
(raise
|
||||||
|
(makeblock 0 (global Match_failure/18!)
|
||||||
|
[0: "example9bis.ml" 4 11])))))
|
||||||
|
(makeblock 0 test/81)))
|
||||||
6
tesi/traces/example9bis.ml
Normal file
|
|
@ -0,0 +1,6 @@
|
||||||
|
[@@@warning "-20"]
|
||||||
|
external observe : 'a -> 'b = "observe"
|
||||||
|
|
||||||
|
let test = function
|
||||||
|
| true -> observe 0
|
||||||
|
(* we expect a Match_failure node for 'false' in the lambda representation *)
|
||||||
15
tesi/traces/example9bis.trace
Normal file
|
|
@ -0,0 +1,15 @@
|
||||||
|
Target program decision tree
|
||||||
|
Switch ({ var=AcRoot=param/82; dom=Int [-inf; -1] [1; +inf] v Tag _; }) =
|
||||||
|
Leaf=VConstant:0
|
||||||
|
Switch ({ var=AcRoot=param/82; dom=Int 0; }) =
|
||||||
|
Failure
|
||||||
|
Fallback=None
|
||||||
|
|
||||||
|
|
||||||
|
Source program decision tree
|
||||||
|
Switch AcRoot:{
|
||||||
|
Bool true ->
|
||||||
|
Leaf='Int 0 '
|
||||||
|
} Fallback: Failure
|
||||||
|
|
||||||
|
The two programs are equivalent.
|
||||||
7
tesi/traces/guards2.lambda
Normal file
|
|
@ -0,0 +1,7 @@
|
||||||
|
(setglobal Guards2!
|
||||||
|
(let
|
||||||
|
(ff/82 =
|
||||||
|
(function x/83
|
||||||
|
(if (guard 0a) (observe 1)
|
||||||
|
(if (guard 1) (observe 2) (observe 3)))))
|
||||||
|
(makeblock 0 ff/82)))
|
||||||
8
tesi/traces/guards2.ml
Normal file
|
|
@ -0,0 +1,8 @@
|
||||||
|
[@@@warning "-20"]
|
||||||
|
external observe : 'a -> 'b = "observe"
|
||||||
|
external guard : 'a -> 'b = "guard"
|
||||||
|
|
||||||
|
let ff = function
|
||||||
|
| x when guard () -> observe 1
|
||||||
|
| _ when guard 1 -> observe 2
|
||||||
|
| _ -> observe 3
|
||||||
24
tesi/traces/guards2.trace
Normal file
|
|
@ -0,0 +1,24 @@
|
||||||
|
Target program decision tree
|
||||||
|
Guard (VConstant:0):
|
||||||
|
guard(true) =
|
||||||
|
Leaf=VConstant:1
|
||||||
|
guard(false) =
|
||||||
|
Guard (VConstant:1):
|
||||||
|
guard(true) =
|
||||||
|
Leaf=VConstant:2
|
||||||
|
guard(false) =
|
||||||
|
Leaf=VConstant:3
|
||||||
|
|
||||||
|
Source program decision tree
|
||||||
|
Switch AcRoot:{
|
||||||
|
} Fallback: Guard (Unit ) =
|
||||||
|
guard(true) =
|
||||||
|
Leaf='Int 1 '
|
||||||
|
guard(false) =
|
||||||
|
Guard (Int 1 ) =
|
||||||
|
guard(true) =
|
||||||
|
Leaf='Int 2 '
|
||||||
|
guard(false) =
|
||||||
|
Leaf='Int 3 '
|
||||||
|
|
||||||
|
The two programs are equivalent.
|
||||||