9.7 KiB
Rete A
M master identici e S slave identici di tipo 1.
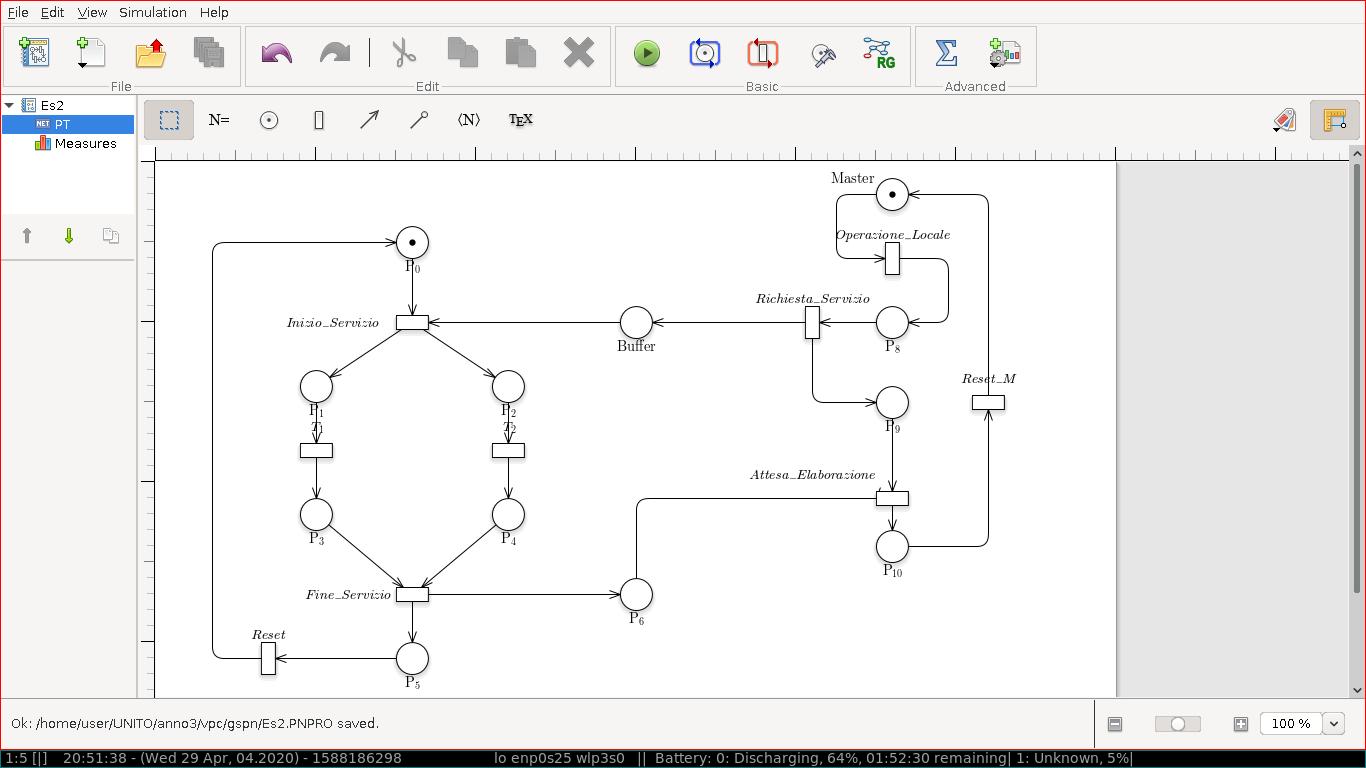
La figura rappresenta la rete di Petri P/T dell'esercizio A. Il master è modellato dai posti M0, M1, M2, M3 e dalle transizioni Azione_Locale, Richiesta_Servizio, Attesa_Elaborazione e Reset_M Lo slave è modellato dai posti S0, S1_a, S1_b, S2_a, S2_b e S3 e dalle transizioni Inizio_Servizio, Azione_Locale_Sa, Azione_Locale_Sb, Fine_Servizio e Reset_S. La richiesta del servizio verso lo slave e` gestita attraverso due buffer, posti Buffer_Input e posto Buffer_Output.
Risultati
Nella tabella vengono mostrate il numero di archi e di nodi al variare dei parametri M e S. Le cifre sono indicative dell'aumentare della dimensione dello spazio degli stati proporzionalmente al numero di marcature.
| master, slaves | Nodi | Archi |
|---|---|---|
| 1, 1 | 14 | 19 |
| 2, 2 | 94 | 222 |
| 3, 3 | 426 | 334 |
| 4, 4 | 1500 | 5610 |
| 5, 5 | 4422 | 18720 |
| 6, 6 | 11418 | 52998 |
| 7, 7 | 26598 | 132594 |
| 8, 8 | 57057 | 301158 |
| 9, 9 | 114400 | 632775 |
| 10, 10 | 216788 | 1246960 |
| 11, 11 | 391612 | 2328612 |
| 12, 12 | 678912 | 4153916 |
| 13, 13 | 1135668 | 7123272 |
| 14, 14 | 1841100 | 11802420 |
| 15, 15 | 2903124 | 18973020 |
Considerazioni su Fork/Join
Il modello non garantisce che avvenga il join di due processi dello stesso padre quando la marcatura degli slave e` maggiore di 2. Si puo` garantire che avvenga il join di due processi forkati dallo stesso padre nei seguenti modi:
- attraverso differenti strutture slaves
- permettendo l'elaborazione di una singola richiesta alla volta (modellato con degli archi inibitori)
- usando reti WN
Riduzione
Una rete di petri puo` essere ridotta usando le seguendi tecniche:
- fusione
- eliminazione
- rimozione dei loop
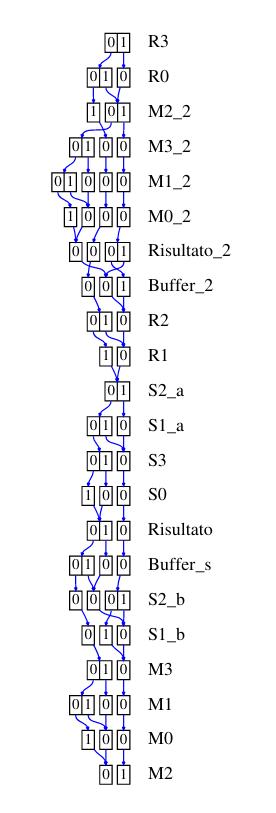
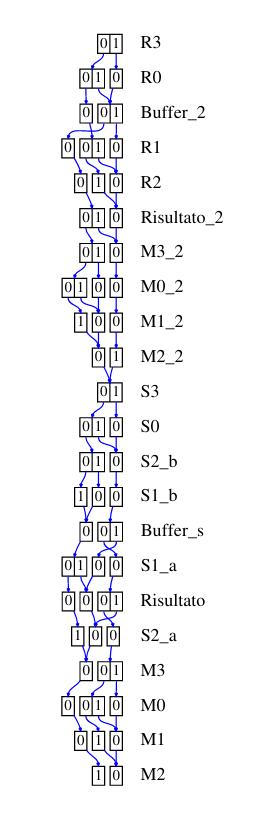
Nelle figure vengono mostrate alcune fasi di riduzione della rete in analisi; in ordine sono stati applicati:
- fusione di alcuni posti
- fusione di alcune transizioni
- eliminazione di alcuni posti
- eliminazione di alcune transizioni
- riduzione di self loop





TODO P e T invarianti
Tramite GreatSPN possiamo calcolare gli T- e P- semiflussi
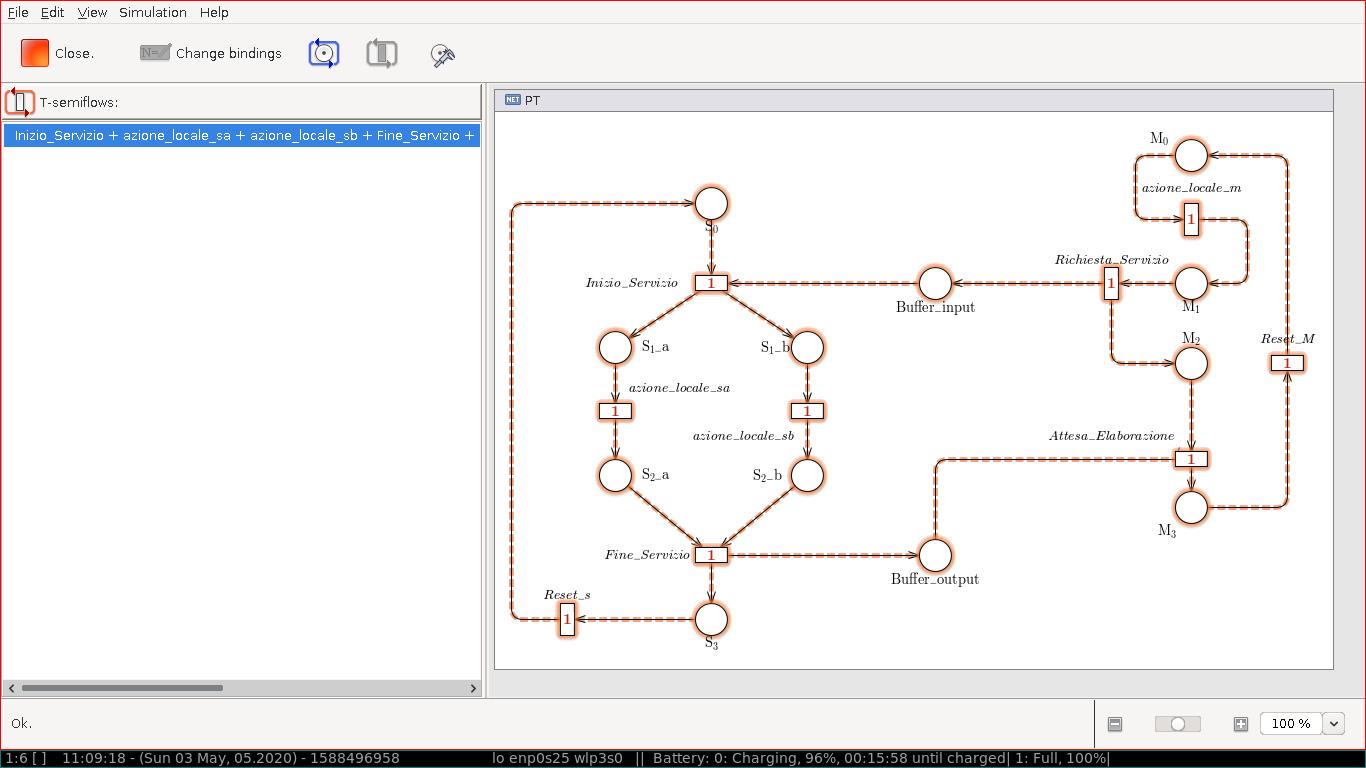
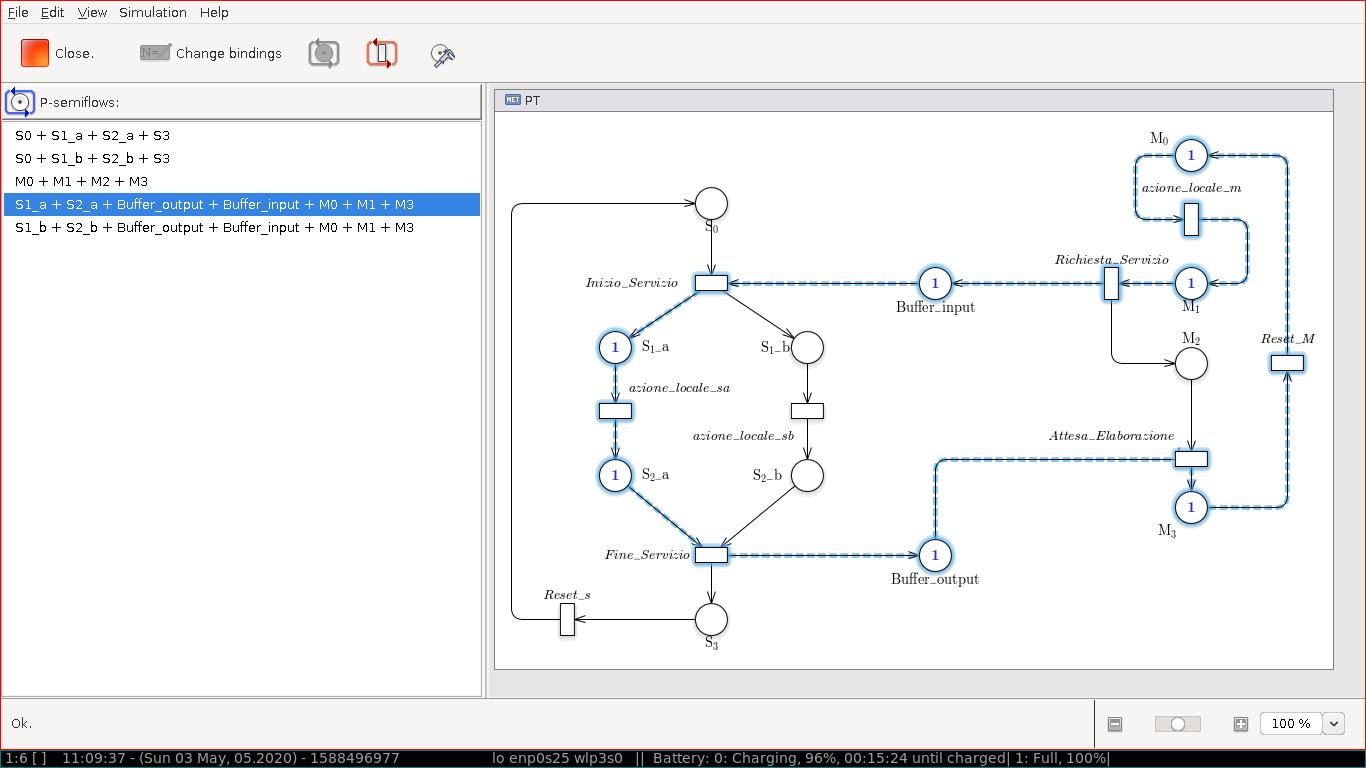
Gli P-invarianti sono i seguenti:
| S0 + S1_a + S2_a + S3 |
| S0 + S1_b + S2_b + S3 |
| M0 + M1 + M2 + M3 |
| S1_a + S2_a + Buffer_output + Buffer_input + M0 + M1 + M3 |
| S1_b + S2_b + Buffer_output + Buffer_input + M0 + M1 + M3 |
Il T-invariante e` il seguento: \[ Inizio_servizio + azione_locale_sa + azione_locale_sb + \\ Fine_servizio + Reset_s + azione_locale_m + Richiesta_servizio + \\ Attesa_elaborazione + Reset_m + Reset_s \]
Dato che la reteA e` interamente coperta dagli P-semiflussi, possiamo affermare che la rete sia bounded. [ ] Deadlock [ ] Liveness
Rete B
M master identici, uno slave di tipo 1 e uno slave di tipo 1 scelti liberamente dai master.
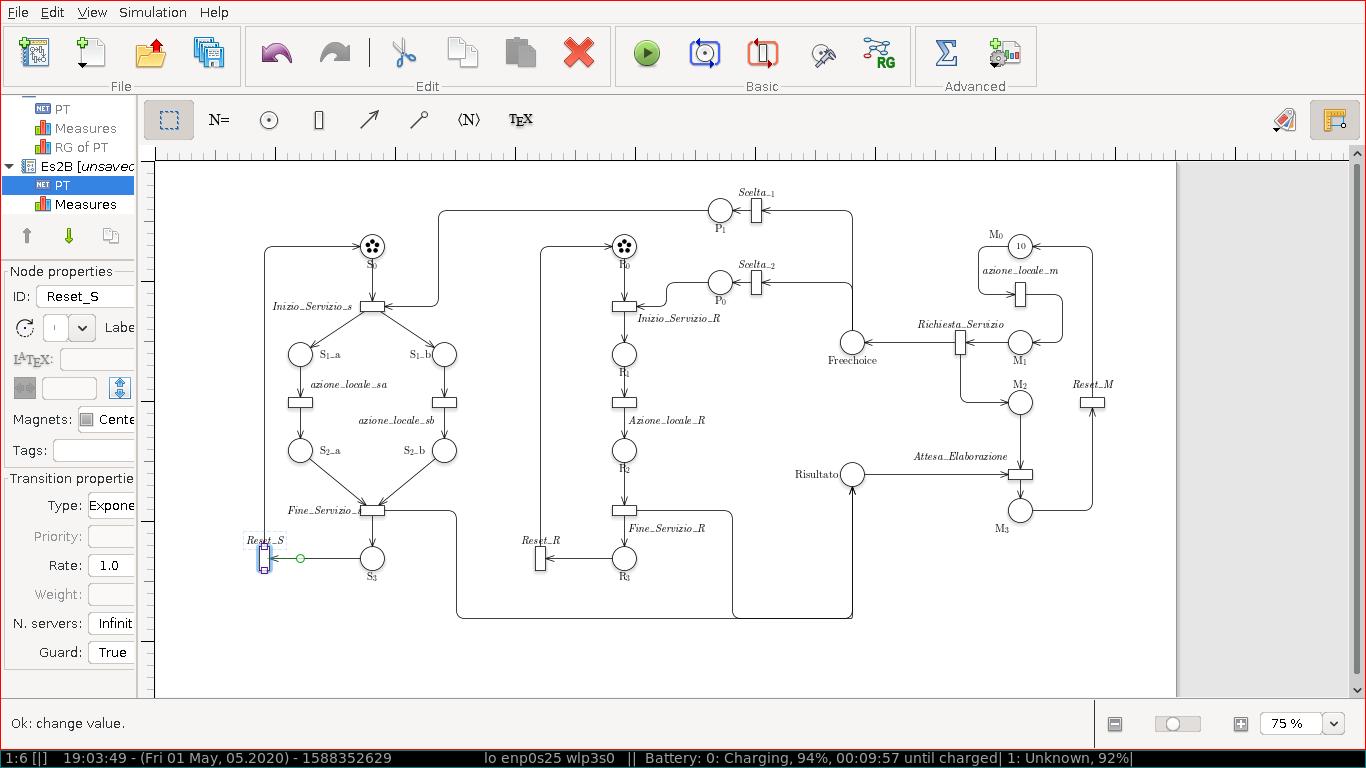
La figura rappresenta la rete di Petri P/T dell'esercizio B. Il master è modellato dai posti M0, M1, M2, M3 e dalle transizioni Azione_Locale, Richiesta_Servizio, Attesa_Elaborazione e Reset_M Lo slave di tipo 1 è modellato dai posti S0, S1_a, S1_b, S2_a, S2_b e S3 e dalle transizioni Inizio_Servizio, Azione_Locale_Sa, Azione_Locale_Sb, Fine_Servizio e Reset_S. Lo slave di tipo 2 è modellato dai posti R0, R1_a, R1_b, R2_a, R2_b e R3 e dalle transizioni Inizio_Servizio_R, Azione_Locale_R, Fine_Servizio e Reset_R. La richiesta del servizio verso lo slave scelto e` gestita attraverso due buffer, posti FreeChoice e Risultato.
Risultati
| master, slaves | Stati | Archi |
|---|---|---|
| 1, 2 | 40 | 76 |
| 2, 2 | 204 | 544 |
| 3, 2 | 728 | 2400 |
| 4, 2 | 2072 | 7896 |
| 5, 2 | 5040 | 21336 |
| 6, 2 | 10920 | 50064 |
| 7, 2 | 21648 | 105648 |
| 8, 2 | 39996 | 205260 |
| 9, 2 | 69784 | 373252 |
| 10, 2 | 116116 | 642928 |
Parametrizzando anche il numero di slaves:
| master, slaves | Stati | Archi |
|---|---|---|
| 1, 2 | 40 | 76 |
| 2, 2 | 204 | 544 |
| 4, 4 | 7265 | 32674 |
| 6, 6 | 113464 | 664234 |
| 8, 8 | 1073226 | 7405654 |
| 10, 10 | 7212128 | 55762000 |
Considerazioni su Fork/Join
Lo slave di tipo 1 processa una sola richiesta alla volta. Il master in attesa del risultato (M2) potrebbe ricevere il risultato di un lavoro richiesto da un altro master.
TODO P e T invarianti
Tramite GreatSPN possiamo calcolare gli T- e P- semiflussi
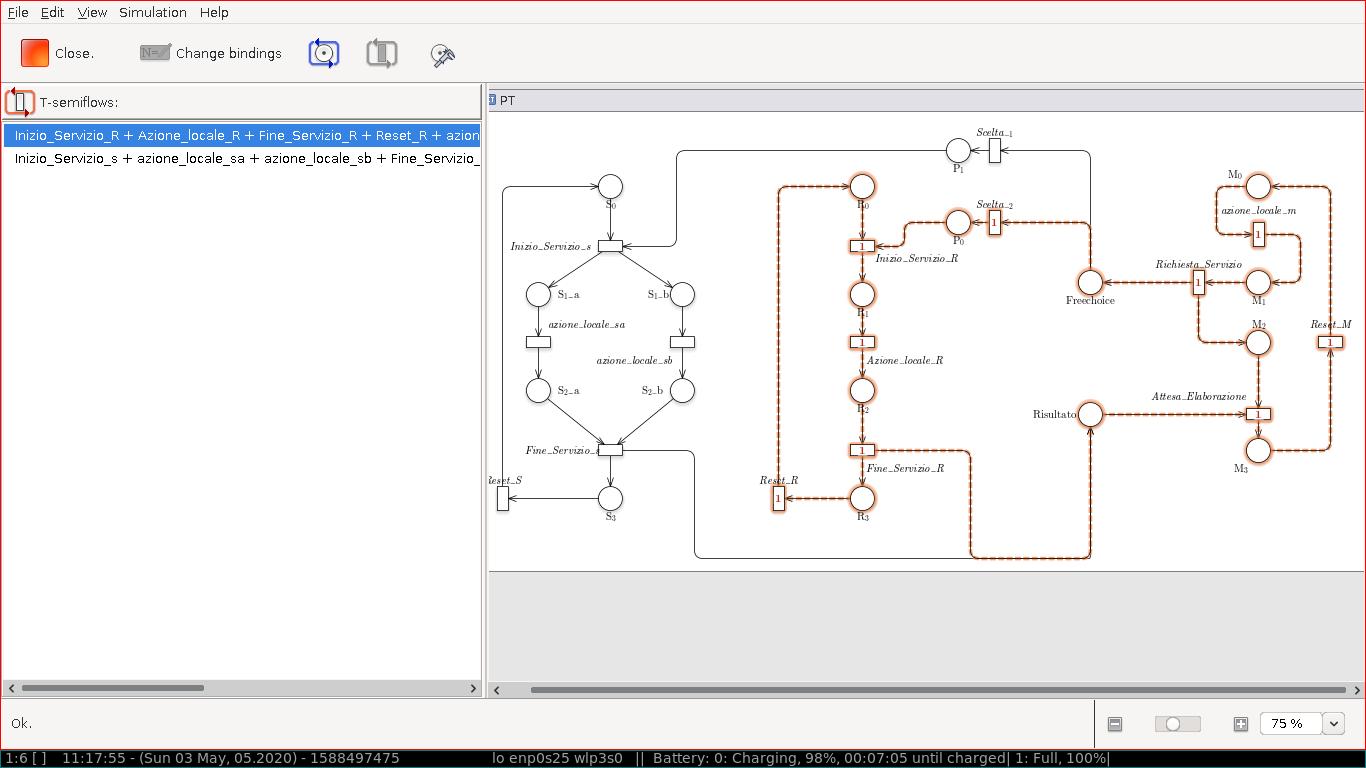
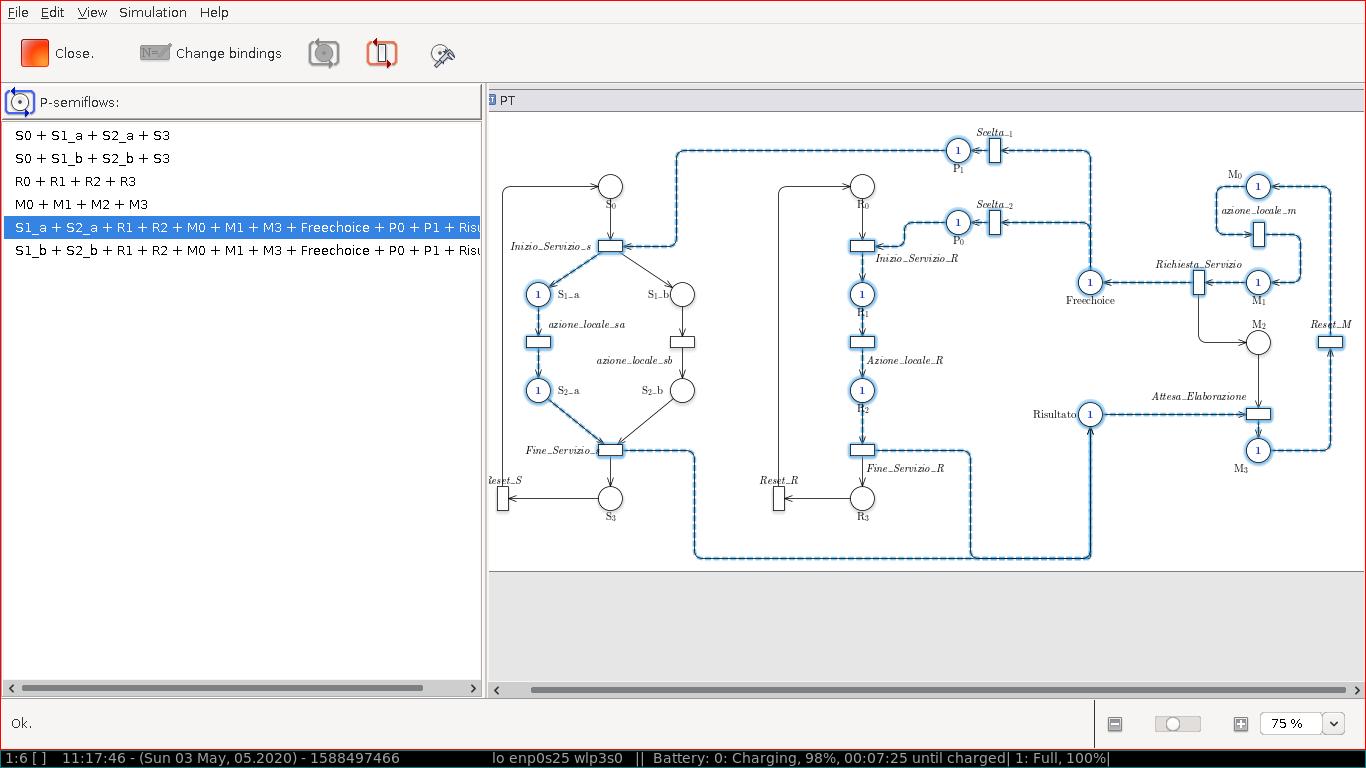
Gli P-invarianti sono i seguenti:
| S0 + S1_a + S2_a + S3 |
| S0 + S1_b + S2_b + S3 |
| R0 + R1 + R2 + R3 |
| M0 + M1 + M2 + M3 |
| S1_a + S2_a + R1 + R2 + M0 + M1 + M3 + Freechoice + P0 + P1 + Risultato |
| S1_b + S2_b + R1 + R2 + M0 + M1 + M3 + Freechoice + P0 + P1 + Risultbto |
Gli T-invarianti sono i seguenti: \[ Inizio_servizio_R + azione_locale_R + \\ Fine_servizio_R + Reset_R + azione_locale_m + Richiesta_servizio + \\ Attesa_elaborazione + Reset_M + Scelta_2 \] \[ Inizio_servizio_S + azione_locale_sa + azione_locale_sb + \\ Fine_servizio_S + Reset_s + azione_locale_m + Richiesta_servizio + \\ Attesa_elaborazione + Reset_m + Scelta_1 \]
Dato che la reteB e` interamente coperta dagli P-semiflussi, possiamo affermare che la rete sia bounded. [ ] Deadlock [ ] Liveness
Rete C
Due master identici, uno slave di tipo 1 e uno slave di tipo 1 scelti liberamente dai master.
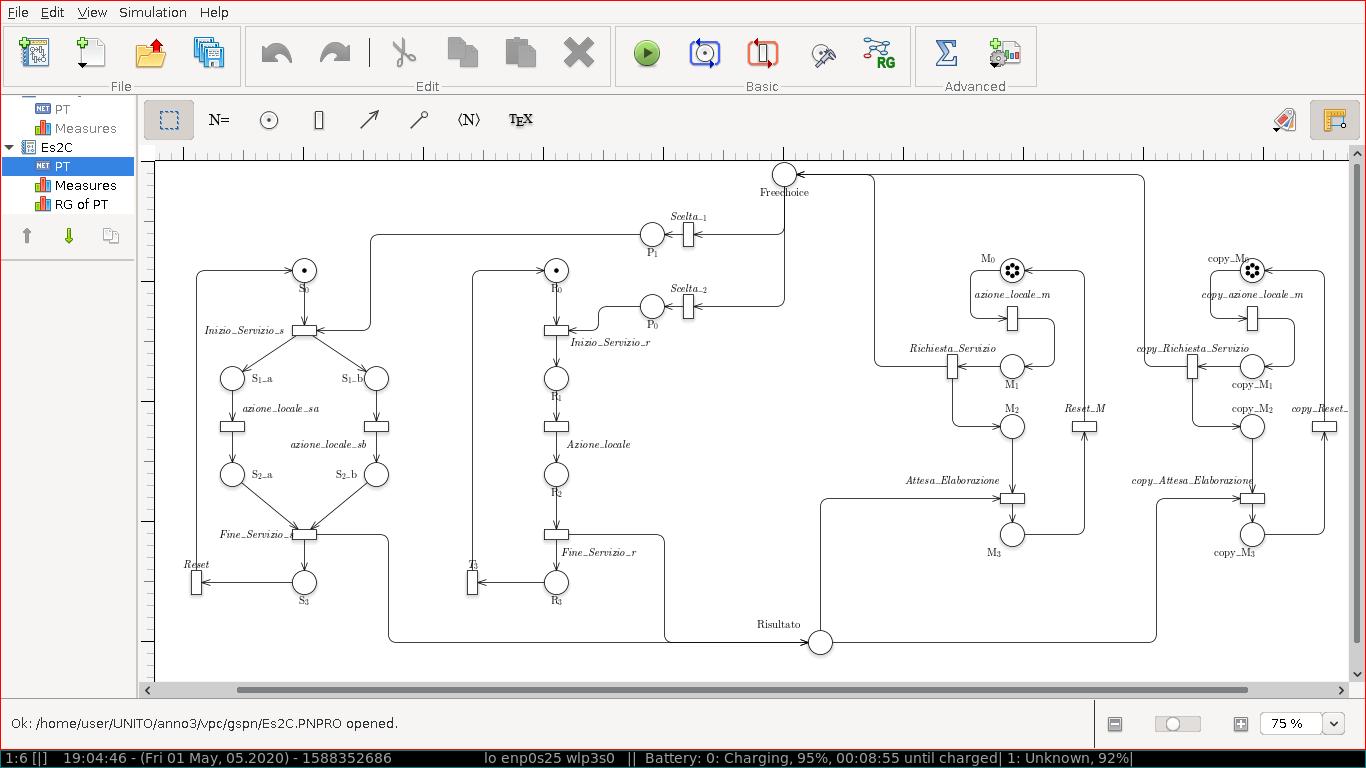
La figura rappresenta la rete di Petri P/T dell'esercizio C. Il master è modellato dai posti M0, M1, M2, M3 e dalle transizioni Azione_Locale, Richiesta_Servizio, Attesa_Elaborazione e Reset_M Lo slave di tipo 1 è modellato dai posti S0, S1_a, S1_b, S2_a, S2_b e S3 e dalle transizioni Inizio_Servizio, Azione_Locale_Sa, Azione_Locale_Sb, Fine_Servizio e Reset_S (il secondo master e` una copia del primo). Lo slave di tipo 2 è modellato dai posti R0, R1_a, R1_b, R2_a, R2_b e R3 e dalle transizioni Inizio_Servizio_R, Azione_Locale_R, Fine_Servizio e Reset_R. La richiesta del servizio verso lo slave scelto e` gestita attraverso due buffer, posti FreeChoice e Risultato.
TODO P e T invarianti
Tramite GreatSPN possiamo calcolare gli T- e P- semiflussi
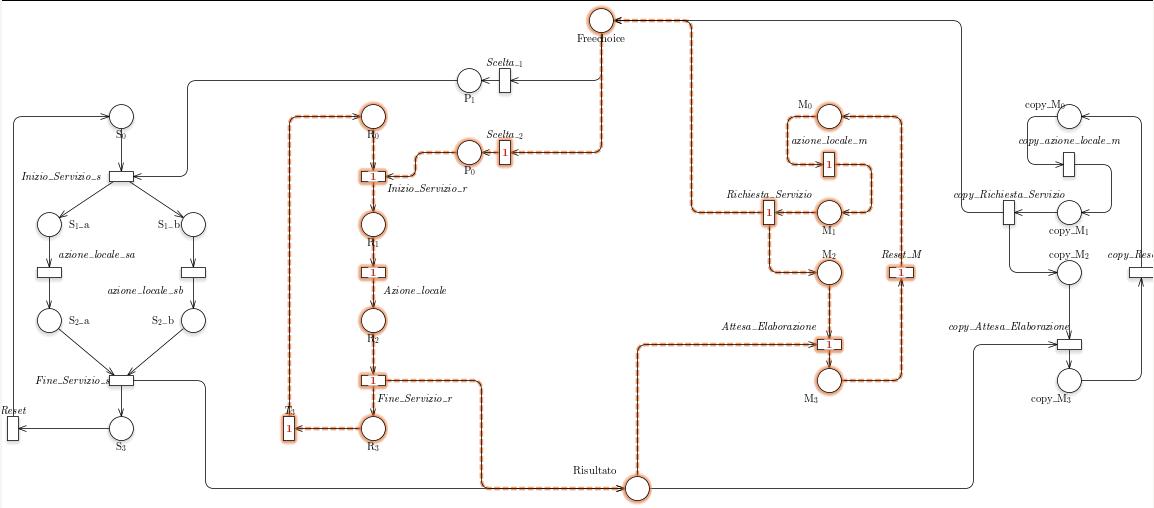
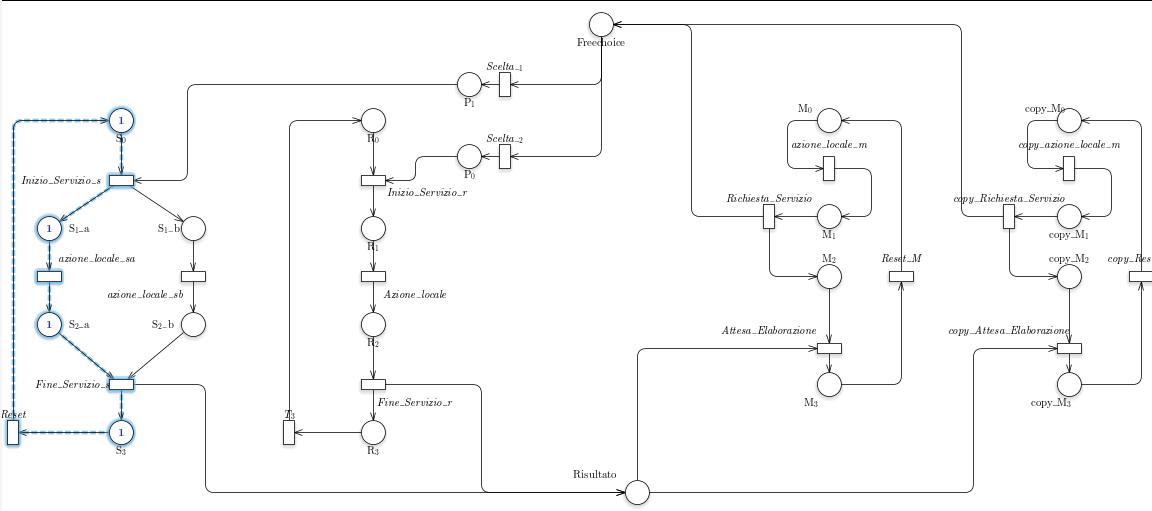
Gli P-invarianti sono i seguenti:
- S0 + S1ₐ + S2ₐ + S3
- S0 + S1b + S2b + S3
- R0 + R1 + R2 + R3
- M0 + M1 + M2 + M3
- copy_M0 + copy_M1 + copy_M2 + copy_M3
- S1ₐ + S2ₐ + R1 + R2 + M0 + M1 + M3 + Freechoice + P0 + P1 + Risultato + copy_M0 + copy_M1 + copy_M3
- S1b + S2b + R1 + R2 + M0 + M1 + M3 + Freechoice + P0 + P1 + Risultato + copy_M0 + copy_M1 + copy_M3
Gli T-invarianti sono i seguenti:
- Inizio_Servizioᵣ + Azione_Locale + Fine_Servizioᵣ + T3 + azione_localeₘ + Richiesta_Servizio + Attesa_Elaborazione + Reset_M + Scelta₁
- Inizio_Servizioₛ + Azione_Localesa + Azione_Localesb + Fine_Servizioₛ + T3 + azione_localeₘ + Richiesta_Servizio + Attesa_Elaborazione + Reset_M + Scelta₁
- Inizio_Servizioᵣ + Azione_Locale + Fine_Servizioᵣ + T3 + Scelta₂ + copyₐzione_localeₘ + copy_Richiesta_Servizio + copy_Attesa_Elaborazione + copy_Resetₘ
- Inizio_Servizioₛ + Azione_Localesa + Azione_Localesb + Fine_Servizioₛ + Reset + Scelta₁ + copy_azione_localeₘ + copy_Richiesta_Servizio + copy_Attesa_Elaborazione + copy_Resetₘ
[ ] Deadlock [ ] Liveness
Rete D
Due master identici, uno slave di tipo 1 e uno slave di tipo 1 scelti associati ciascuno ad un master diverso.
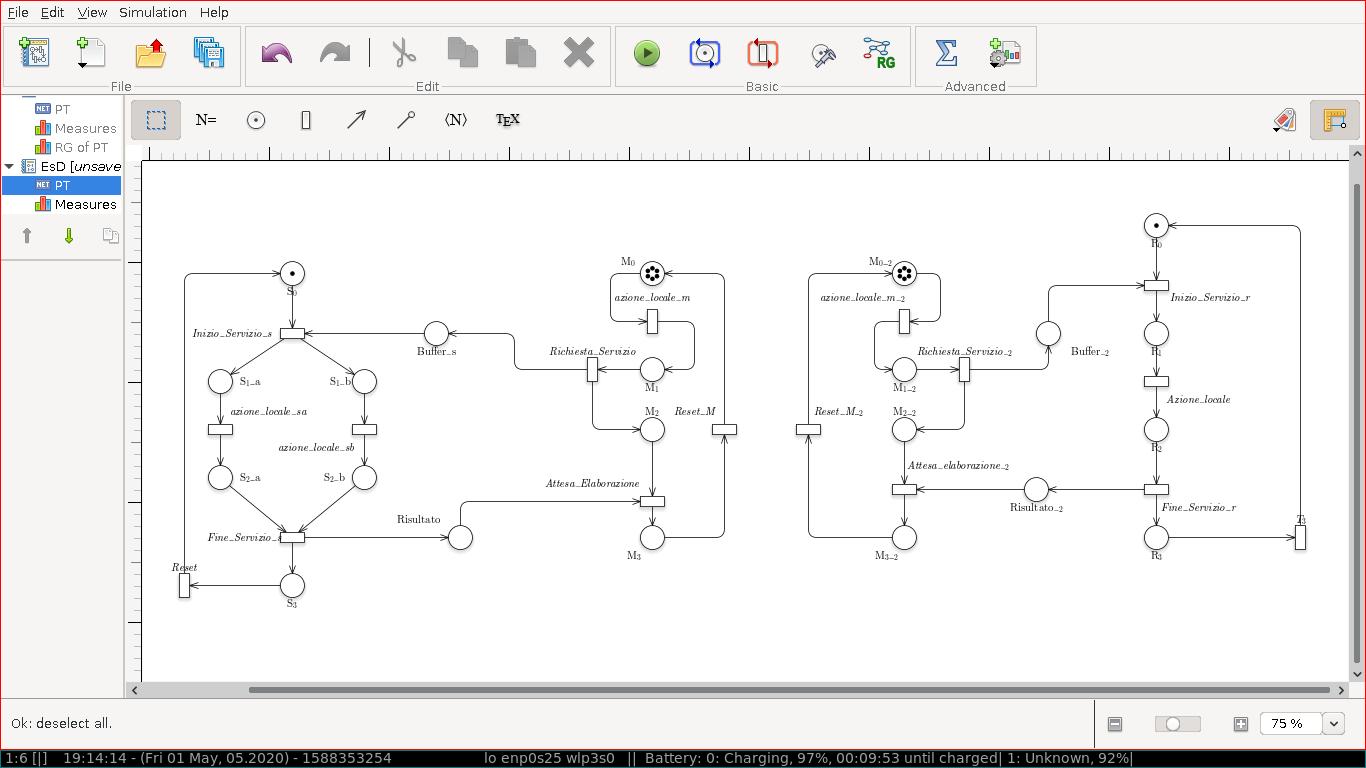
P e T invarianti
Tramite GreatSPN possiamo calcolare gli T- e P- semiflussi
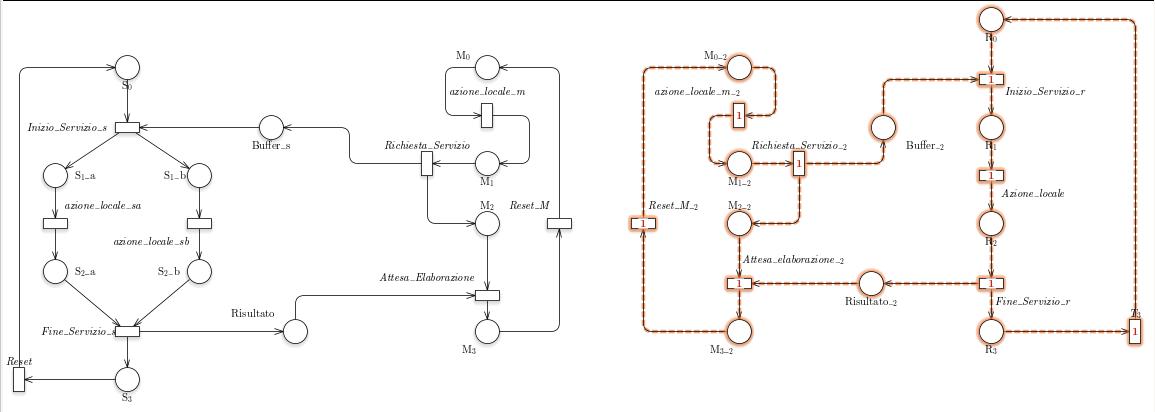
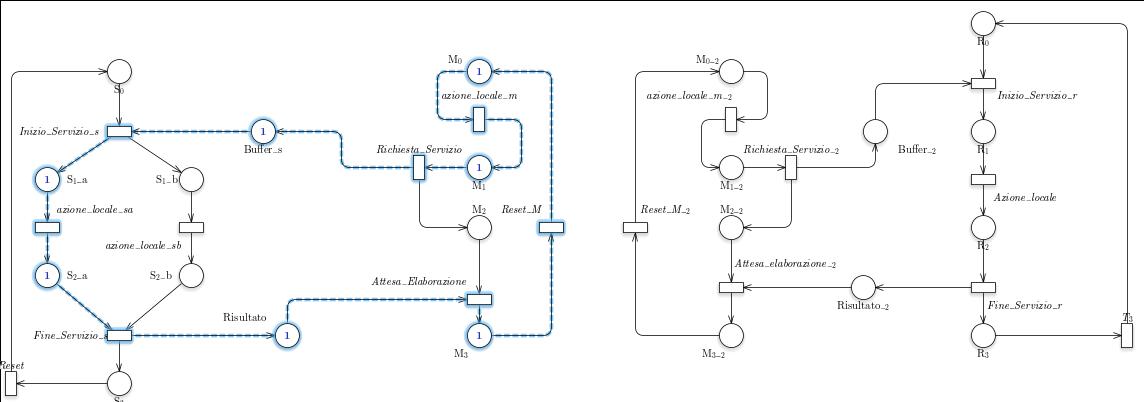
Gli P-invarianti sono i seguenti:
- S0 + S1ₐ + S2ₐ + S3
- S0 + S1b + S2b + S3
- R0 + R1 + R2 + R3
- M0 + M1 + M2 + M3
- S1ₐ + S2ₐ + M0 + M1 + M3 + Bufferₛ + Risultato
- S1b + S2b + M0 + M1 + M3 + Bufferₛ + Risultato
- M0₂ + M1₂ + M3₂
- R1 + R2 + M0₂ + M1₂ + M3₂ + Buffer₂ + Risultato₂
Gli T-invarianti sono i seguenti:
- Inizio_Servizioₛ + azione_localesa + azione_localesb + Fine_Servizioₛ + Reset + azione_localeₘ + Richiesta_Servizio + Attesa_Elaborazione + Resetₘ
- Inizio_Servizioᵣ + Azione_locale + Fine_Servizioᵣ + T3 azione_localem2 + Richiesta_Servizio₂ + Attesa_Elaborazione₂ + Resetm2
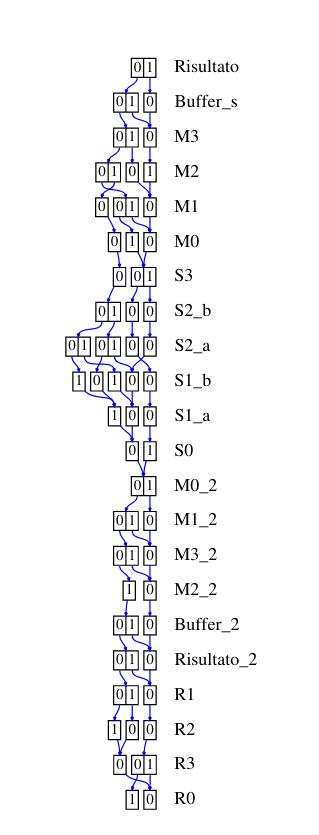
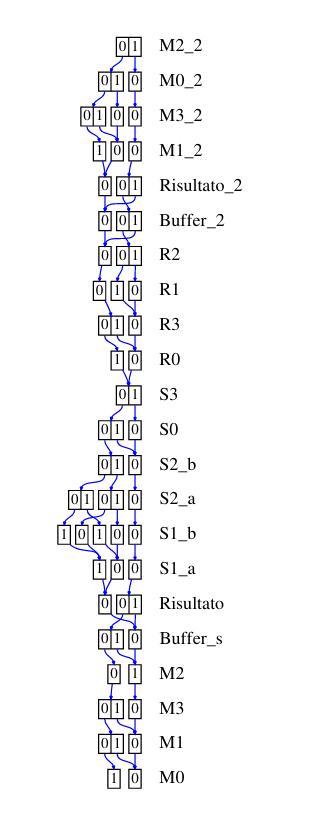
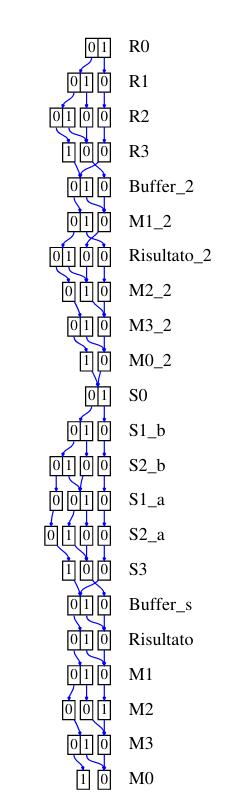
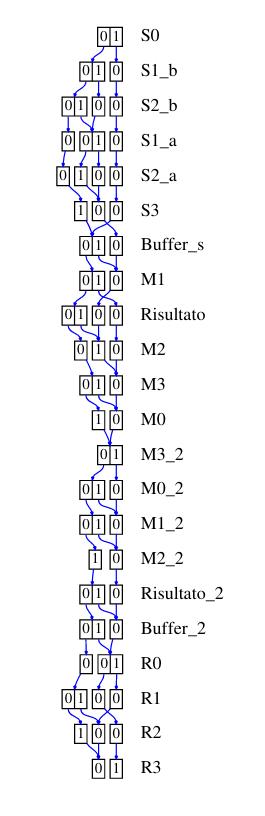
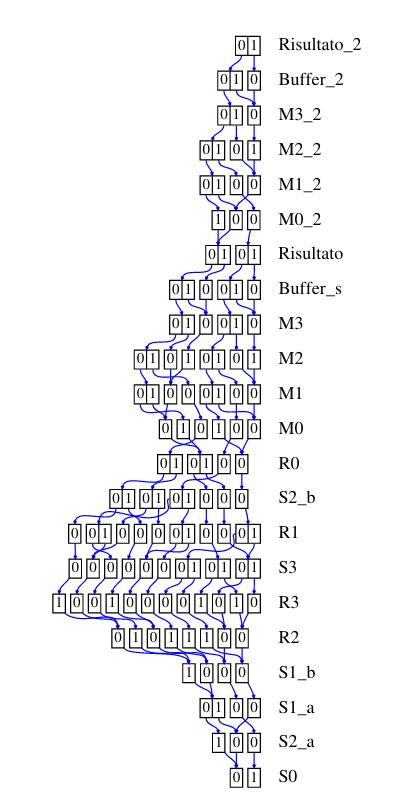
Decision Diagram
L'efficacia dei decision diagram sulla generazione dello stato degli spazi dipende fortemente dall'ordine delle variabili. Di seguito vengono mostrati i decision diagram usando per le assegnazioni i seguenti algoritmi:
- Sloan: un algoritmo di riduzione della banda di matrici sparse con una buona performance
- (advanced) Cuthill-McKee: un altro algoritmo di riduzione della banda di matrici sparse
- Tovchigrechko e Noack: due algoritmo appositamente ideati per le reti di Petri, anch'essi con una buona performance
- P-chaining: un algoritmo che sfrutta le informazioni strutturali della rete ma ha una bassa performance
- Gradient-P
- Gibbs-Poole-Stockmeier: un altro algoritmo matriciale che nella rete in analisi ha restituito il risultato peggiore