73 KiB
Translation Verification of the pattern matching compiler
\begin{comment} TODO: not all todos are explicit. Check every comment section TODO: chiedi a Gabriel se T e S vanno bene, ma prima controlla che siano coerenti * TODO Scaletta [1/5] - [X] Introduction - [-] Background [80%] - [X] Low level representation - [X] Lambda code [0%] - [X] Pattern matching - [X] Symbolic execution - [ ] Translation Validation - [-] Translation validation of the Pattern Matching Compiler - [X] Source translation - [X] Formal Grammar - [X] Compilation of source patterns - [ ] Target translation - [ ] Formal Grammar - [ ] Symbolic execution of the Lambda target - [X] Equivalence between source and target - [ ] Practical results Magari prima pattern matching poi compilatore? \end{comment} \begin{comment} MAIL COPPO: Dovrei usare il termine tool invece di algoritmo? \end{comment} \begin{comment} TODO: Bibliografia! Dolan, altri sulla symexec??? Cita i paper e il libro \end{comment}§ion{Introduction}
This dissertation presents an algorithm for the translation validation of the OCaml pattern matching compiler. Given a source program and its compiled version the algorithm checks whether the two are equivalent or produce a counter example in case of a mismatch. For the prototype of this algorithm we have chosen a subset of the OCaml language and implemented a prototype equivalence checker along with a formal statement of correctness and its proof. The prototype is to be included in the OCaml compiler infrastructure and will aid the development.
Our equivalence algorithm works with decision trees. Source patterns are converted into a decision tree using a matrix decomposition algorithm. Target programs, described in the Lambda intermediate representation language of the OCaml compiler, are turned into decision trees by applying symbolic execution.
\begin{comment} \subsection{Translation validation} \end{comment}A pattern matching compiler turns a series of pattern matching clauses into simple control flow structures such as \texttt{if, switch}, for example:
\begin{lstlisting} match scrutinee with | [] -> (0, None) | x::[] -> (1, Some x) | _::y::_ -> (2, Some y) \end{lstlisting}Given as input to the pattern matching compiler, this snippet of code gets translated into the Lambda intermediate representation of the OCaml compiler. The Lambda representation of a program is shown by calling the \texttt{ocamlc} compiler with \texttt{-drawlambda} flag. In this example we renamed the variables assigned in order to ease the understanding of the tests that are performed when the code is translated into the Lambda form. code phase.
\begin{lstlisting} (function scrutinee (if scrutinee ;;; true when scrutinee (list) not empty (let (tail =a (field 1 scrutinee/81)) ;;; assignment (if tail (let y =a (field 0 tail)) ;;; y is the first element of the tail (makeblock 0 2 (makeblock 0 y))) ;;; allocate memory for tuple (2, Some y) (let (x =a (field 0 scrutinee)) ;;; x is the head of the scrutinee (makeblock 0 1 (makeblock 0 x))))) ;;; allocate memory for tuple (1, Some x) [0: 0 0a]))) ;;; low level representatio of (0, None) \end{lstlisting}The OCaml pattern matching compiler is a critical part of the OCaml compiler in terms of correctness because bugs typically would result in wrong code production rather than triggering compilation failures. Such bugs also are hard to catch by testing because they arise in corner cases of complex patterns which are typically not in the compiler test suite or most user programs.
The OCaml core developers group considered evolving the pattern matching compiler, either by using a new algorithm or by incremental refactoring of its code base. For this reason we want to verify that new implementations of the compiler avoid the introduction of new bugs and that such modifications don't result in a different behavior than the current one.
One possible approach is to formally verify the pattern matching compiler implementation using a machine checked proof. Another possibility, albeit with a weaker result, is to verify that each source program and target program pair are semantically correct. We chose the latter technique, translation validation because is easier to adopt in the case of a production compiler and to integrate with an existing code base. The compiler is treated as a black-box and proof only depends on our equivalence algorithm.
⊂section{Our approach} Our algorithm translates both source and target programs into a common representation, decision trees. Decision trees where chosen because they model the space of possible values at a given branch of execution. Here are the decision trees for the source and target example program.
\begin{minipage}{0.5\linewidth} \scriptsize
\begin{verbatim} Switch(Root) / \ (= []) (= ::) / \ Leaf Switch(Root.1) (0, None) / \ (= []) (= ::) / \ Leaf Leaf [x = Root.0] [y = Root.1.0] (1, Some x) (2, Some y) \end{verbatim}\end{minipage} \hfill \begin{minipage}{0.4\linewidth} \scriptsize
\begin{verbatim} Switch(Root) / \ (= int 0) (!= int 0) / \ Leaf Switch(Root.1) (mkblock 0 / \ 0 0a) / \ (= int 0) (!= int 0) / \ Leaf Leaf [x = Root.0] [y = Root.1.0] (mkblock 0 (mkblock 0 1 (mkblock 0 x)) 2 (mkblock 0 y)) \end{verbatim}\end{minipage}
\texttt{(Root.0)} is called an \emph{accessor}, that represents the access path to a value that can be reached by deconstructing the scrutinee. In this example \texttt{Root.0} is the first subvalue of the scrutinee.
Target decision trees have a similar shape but the tests on the branches are related to the low level representation of values in Lambda code. For example, cons cells \texttt{x::xs} or tuples \texttt{(x,y)} are blocks with tag 0.
To check the equivalence of a source and a target decision tree, we proceed by case analysis. If we have two terminals, such as leaves in the previous example, we check that the two right-hand-sides are equivalent. If we have a node $N$ and another tree $T$ we check equivalence for each child of $N$, which is a pair of a branch condition $\pi_i$ and a subtree $C_i$. For every child $(\pi_i, C_i)$ we reduce $T$ by killing all the branches that are incompatible with $\pi_i$ and check that the reduced tree is equivalent to $C_i$.
⊂section{From source programs to decision trees} Our source language supports integers, lists, tuples and all algebraic datatypes. Patterns support wildcards, constructors and literals, Or-patterns such as $(p_1 | p_2)$ and pattern variables. In particular Or-patterns provide a more compact way to group patterns that point to the same expression.
\begin{minipage}{0.4\linewidth}
\begin{lstlisting} match w with | p₁ -> expr | p₂ -> expr | p₃ -> expr \end{lstlisting}\end{minipage} \begin{minipage}{0.6\linewidth}
\begin{lstlisting} match w with | p₁|p₂|p₃ -> expr \end{lstlisting}\end{minipage} We also support \texttt{when} guards, which are interesting as they introduce the evaluation of expressions during matching. This is the type definition of decision tree as they are used in the prototype implementation:
\begin{lstlisting} type decision_tree = | Unreachable | Failure | Leaf of source_expr | Guard of source_expr * decision_tree * decision_tree | Switch of accessor * (constructor * decision_tree) list * decision_tree \end{lstlisting}In the \texttt{Switch} node we have one subtree for every head constructor that appears in the pattern matching clauses and a fallback case for other values. The branch condition $\pi_i$ expresses that the value at the switch accessor starts with the given constructor. \texttt{Failure} nodes express match failures for values that are not matched by the source clauses. \texttt{Unreachable} is used when we statically know that no value can flow to that subtree.
We write 〚tₛ〛ₛ to denote the translation of the source program (the set of pattern matching clauses) into a decision tree, computed by a matrix decomposition algorithm (each column decomposition step gives a \texttt{Switch} node). It satisfies the following correctness statement: \[ \forall t_s, \forall v_s, \quad t_s(v_s) = \semTEX{t_s}_s(v_s) \] The correctness statement intuitively states that for every source program, for every source value that is well-formed input to a source program, running the program tₛ against the input value vₛ is the same as running the compiled source program 〚tₛ〛 (that is a decision tree) against the same input value vₛ".
⊂section{From target programs to decision trees} The target programs include the following Lambda constructs: \texttt{let, if, switch, Match\_failure, catch, exit, field} and various comparison operations, guards. The symbolic execution engine traverses the target program and builds an environment that maps variables to accessors. It branches at every control flow statement and emits a \texttt{Switch} node. The branch condition $\pi_i$ is expressed as an interval set of possible values at that point. In comparison with the source decision trees, \texttt{Unreachable} nodes are never emitted. Guards result in branching. In comparison with the source decision trees, \texttt{Unreachable} nodes are never emitted.
We write $\semTEX{t_T}_T$ to denote the translation of a target program tₜ into a decision tree of the target program $t_T$, satisfying the following correctness statement that is simmetric to the correctness statement for the translation of source programs: \[ \forall t_T, \forall v_T, \quad t_T(v_T) = \semTEX{t_T}_T(v_T) \]
⊂section{Equivalence checking} The equivalence checking algorithm takes as input a domain of possible values \emph{S} and a pair of source and target decision trees and in case the two trees are not equivalent it returns a counter example. Our algorithm respects the following correctness statement:
\begin{comment} % TODO: we have to define what \coversTEX mean for readers to understand the specifications % (or we use a simplifying lie by hiding \coversTEX in the statements). \end{comment} \begin{align*} \EquivTEX S {C_S} {C_T} = \YesTEX \;\land\; \coversTEX {C_T} S & \implies \forall v_S \approx v_T \in S,\; C_S(v_S) = C_T(v_T) \\ \EquivTEX S {C_S} {C_T} = \NoTEX {v_S} {v_T} \;\land\; \coversTEX {C_T} S & \implies v_S \approx v_T \in S \;\land\; C_S(v_S) \neq C_T(v_T) \end{align*}The algorithm proceeds by case analysis. Inference rules are shown. If $S$ is empty the results is $\YesTEX$.
\begin{mathpar} \infer{ } {\EquivTEX \emptyset {C_S} {C_T} G} \end{mathpar}If the two decision trees are both terminal nodes the algorithm checks for content equality.
\begin{mathpar} \infer{ } {\EquivTEX S \Failure \Failure \emptyqueue} \\ \infer {\trel {t_S} {t_T}} {\EquivTEX S {\Leaf {t_S}} {\Leaf {t_T}} \emptyqueue} \end{mathpar}If the source decision tree (left hand side) is a terminal while the target decisiorn tree (right hand side) is not, the algorithm proceeds by \emph{explosion} of the right hand side. Explosion means that every child of the right hand side is tested for equality against the left hand side.
\begin{mathpar} \infer {C_S \in {\Leaf t, \Failure} \\ \forall i,\; \EquivTEX {(S \land a \in D_i)} {C_S} {C_i} G \\ \EquivTEX {(S \land a \notin \Fam i {D_i})} {C_S} \Cfb G} {\EquivTEX S {C_S} {\Switch a {\Fam i {D_i} {C_i}} \Cfb} G} \end{mathpar} \begin{comment} % TODO: [Gabriel] in practice the $dom_S$ are constructors and the % $dom_T$ are domains. Do we want to hide this fact, or be explicit % about it? (Maybe we should introduce explicitly/clearly the idea of % target domains at some point). \end{comment}When the left hand side is not a terminal, the algorithm explodes the left hand side while trimming every right hand side subtree. Trimming a left hand side tree on an interval set $dom_S$ computed from the right hand side tree constructor means mapping every branch condition $dom_T$ (interval set of possible values) on the left to the intersection of $dom_T$ and $dom_S$ when the accessors on both side are equal, and removing the branches that result in an empty intersection. If the accessors are different, \emph{$dom_T$} is left unchanged.
\begin{mathpar} \infer {\forall i,\; \EquivTEX {(S \land a = K_i)} {C_i} {\trim {C_T} {a = K_i}} G \\ \EquivTEX {(S \land a \notin \Fam i {K_i})} \Cfb {\trim {C_T} {a \notin \Fam i {K_i}}} G } {\EquivTEX S {\Switch a {\Fam i {K_i, C_i}} \Cfb} {C_T} G} \end{mathpar}The equivalence checking algorithm deals with guards by storing a queue. A guard blackbox is pushed to the queue whenever the algorithm encounters a Guard node on the right, while it pops a blackbox from the queue whenever a Guard node appears on the left hand side. The algorithm stops with failure if the popped blackbox and the and blackbox on the left hand Guard node are different, otherwise in continues by exploding to two subtrees, one in which the guard condition evaluates to true, the other when it evaluates to false. Termination of the algorithm is successful only when the guards queue is empty.
\begin{mathpar} \infer {\EquivTEX S {C_0} {C_T} {G, (t_S = 0)} \\ \EquivTEX S {C_1} {C_T} {G, (t_S = 1)}} {\EquivTEX S {\Guard {t_S} {C_0} {C_1}} {C_T} G} \infer {\trel {t_S} {t_T} \\ \EquivTEX S {C_S} {C_b} G} {\EquivTEX S {C_S} {\Guard {t_T} {C_0} {C_1}} {(t_S = b), G}} \end{mathpar} \begin{comment} TODO: replace inference rules with good latex \end{comment}Background
OCaml
Objective Caml (OCaml) is a dialect of the ML (Meta-Language) family of programming that features with other dialects of ML, such as SML and Caml Light. The main features of ML languages are the use of the Hindley-Milner type system that provides many advantages with respect to static type systems of traditional imperative and object oriented language such as C, C++ and Java, such as:
- Polymorphism: in certain scenarios a function can accept more than one type for the input parameters. For example a function that computes the length of a list doesn't need to inspect the type of the elements of the list and for this reason a List.length function can accept lists of integers, lists of strings and in general lists of any type. Such languages offer polymorphic functions through subtyping at runtime only, while other languages such as C++ offer polymorphism through compile time templates and function overloading. With the Hindley-Milner type system each well typed function can have more than one type but always has a unique best type, called the principal type. For example the principal type of the List.length function is "For any a, function from list of a to int" and a is called the type parameter.
- Strong typing: Languages such as C and C++ allow the programmer to operate on data without considering its type, mainly through pointers. Other languages such as C# and Go allow type erasure so at runtime the type of the data can't be queried. In the case of programming languages using an Hindley-Milner type system the programmer is not allowed to operate on data by ignoring or promoting its type.
- Type Inference: the principal type of a well formed term can be inferred without any annotation or declaration.
- Algebraic data types: types that are modeled by the use of two algebraic operations, sum and product. A sum type is a type that can hold of many different types of objects, but only one at a time. For example the sum type defined as A + B can hold at any moment a value of type A or a value of type B. Sum types are also called tagged union or variants. A product type is a type constructed as a direct product of multiple types and contains at any moment one instance for every type of its operands. Product types are also called tuples or records. Algebraic data types can be recursive in their definition and can be combined.
Moreover ML languages are functional, meaning that functions are treated as first class citizens and variables are immutable, although mutable statements and imperative constructs are permitted. In addition to that features an object system, that provides inheritance, subtyping and dynamic binding, and modules, that provide a way to encapsulate definitions. Modules are checked statically and can be reifycated through functors.
Compiling OCaml code
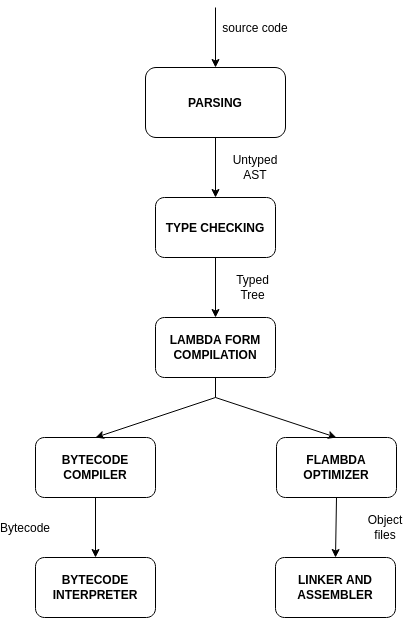
The OCaml compiler provides compilation of source files in form of a bytecode executable with an optionally embeddable interpreter or as a native executable that could be statically linked to provide a single file executable. Every source file is treated as a separate compilation unit that is advanced through different states. The first stage of compilation is the parsing of the input code that is trasformed into an untyped syntax tree. Code with syntax errors is rejected at this stage. After that the AST is processed by the type checker that performs three steps at once:
- type inference, using the classical Algorithm W
- perform subtyping and gathers type information from the module system
- ensures that the code obeys the rule of the OCaml type system
At this stage, incorrectly typed code is rejected. In case of success, the untyped AST in trasformed into a Typed Tree. After the typechecker has proven that the program is type safe, the compiler lower the code to Lambda, an s-expression based language that assumes that its input has already been proved safe. After the Lambda pass, the Lambda code is either translated into bytecode or goes through a series of optimization steps performed by the Flambda optimizer before being translated into assembly.
\begin{comment} TODO: Talk about flambda passes? \end{comment}
This is an overview of the different compiler steps.
Memory representation of OCaml values
An usual OCaml source program contains few to none explicit type signatures. This is possible because of type inference that allows to annotate the AST with type informations. However, since the OCaml typechecker guarantes that a program is well typed before being transformed into Lambda code, values at runtime contains only a minimal subset of type informations needed to distinguish polymorphic values. For runtime values, OCaml uses a uniform memory representation in which every variable is stored as a value in a contiguous block of memory. Every value is a single word that is either a concrete integer or a pointer to another block of memory, that is called cell or box. We can abstract the type of OCaml runtime values as the following:
type t = Constant | Cell of int * twhere a one bit tag is used to distinguish between Constant or Cell. In particular this bit of metadata is stored as the lowest bit of a memory block.
Given that all the OCaml target architectures guarantee that all pointers are divisible by four and that means that two lowest bits are always 00 storing this bit of metadata at the lowest bit allows an optimization. Constant values in OCaml, such as integers, empty lists, Unit values and constructors of arity zero (constant constructors) are unboxed at runtime while pointers are recognized by the lowest bit set to 0.
Lambda form compilation
A Lambda code target file is produced by the compiler and consists of a single s-expression. Every s-expression consist of (, a sequence of elements separated by a whitespace and a closing ). Elements of s-expressions are:
- Atoms: sequences of ascii letters, digits or symbols
- Variables
- Strings: enclosed in double quotes and possibly escaped
- S-expressions: allowing arbitrary nesting
The Lambda form is a key stage where the compiler discards type informations and maps the original source code to the runtime memory model described. In this stage of the compiler pipeline pattern match statements are analyzed and compiled into an automata.
\begin{comment} evidenzia centralita` rispetto alla tesi \end{comment}type t = | Foo | Bar | Baz | Fred
let test = function
| Foo -> "foo"
| Bar -> "bar"
| Baz -> "baz"
| Fred -> "fred"The Lambda output for this code can be obtained by running the compiler with the -dlambda flag:
(setglobal Prova!
(let
(test/85 =
(function param/86
(switch* param/86
case int 0: "foo"
case int 1: "bar"
case int 2: "baz"
case int 3: "fred")))
(makeblock 0 test/85)))As outlined by the example, the makeblock directive is responsible for allocating low level OCaml values and every constant constructor ot the algebraic type t is stored in memory as an integer. The setglobal directives declares a new binding in the global scope: Every concept of modules is lost at this stage of compilation. The pattern matching compiler uses a jump table to map every pattern matching clauses to its target expression. Values are addressed by a unique name.
type t = | English of p | French of q
type p = | Foo | Bar
type q = | Tata| Titi
type t = | English of p | French of q
let test = function
| English Foo -> "foo"
| English Bar -> "bar"
| French Tata -> "baz"
| French Titi -> "fred"In the case of types with a smaller number of variants, the pattern matching compiler may avoid the overhead of computing a jump table. This example also highlights the fact that non constant constructor are mapped to cons cell that are accessed using the tag directive.
(setglobal Prova!
(let
(test/89 =
(function param/90
(switch* param/90
case tag 0: (if (!= (field 0 param/90) 0) "bar" "foo")
case tag 1: (if (!= (field 0 param/90) 0) "fred" "baz"))))
(makeblock 0 test/89)))In the Lambda language are several numeric types:
- integers: that us either 31 or 63 bit two's complement arithmetic depending on system word size, and also wrapping on overflow
- 32 bit and 64 bit integers: that use 32-bit and 64-bit two's complement arithmetic with wrap on overflow
- big integers: offer integers with arbitrary precision
- floats: that use IEEE754 double-precision (64-bit) arithmetic with the addition of the literals infinity, neg_infinity and nan.
The are various numeric operations defined:
- Arithmetic operations: +, -, *, /, % (modulo), neg (unary negation)
- Bitwise operations: &, |, ^, <<, >> (zero-shifting), a>> (sign extending)
- Numeric comparisons: <, >, <=, >=, ==
Functions
Functions are defined using the following syntax, and close over all bindings in scope: (lambda (arg1 arg2 arg3) BODY) and are applied using the following syntax: (apply FUNC ARG ARG ARG) Evaluation is eager.
Other atoms
The atom let introduces a sequence of bindings at a smaller scope than the global one: (let BINDING BINDING BINDING … BODY)
The Lambda form supports many other directives such as strinswitch that is constructs aspecialized jump tables for string, integer range comparisons and so on. These construct are explicitely undocumented because the Lambda code intermediate language can change across compiler releases.
\begin{comment} Spiega che la sintassi che supporti e` quella nella BNF \end{comment}Pattern matching
Pattern matching is a widely adopted mechanism to interact with ADT. C family languages provide branching on predicates through the use of if statements and switch statements. Pattern matching on the other hands express predicates through syntactic templates that also allow to bind on data structures of arbitrary shapes. One common example of pattern matching is the use of regular expressions on strings. provides pattern matching on ADT and primitive data types. The result of a pattern matching operation is always one of:
- this value does not match this pattern”
- this value matches this pattern, resulting the following bindings of names to values and the jump to the expression pointed at the pattern.
type color = | Red | Blue | Green | Black | White
match color with
| Red -> print "red"
| Blue -> print "red"
| Green -> print "red"
| _ -> print "white or black"provides tokens to express data destructoring. For example we can examine the content of a list with pattern matching
begin match list with
| [ ] -> print "empty list"
| element1 :: [ ] -> print "one element"
| (element1 :: element2) :: [ ] -> print "two elements"
| head :: tail-> print "head followed by many elements"Parenthesized patterns, such as the third one in the previous example, matches the same value as the pattern without parenthesis.
The same could be done with tuples
begin match tuple with
| (Some _, Some _) -> print "Pair of optional types"
| (Some _, None) | (None, Some _) -> print "Pair of optional types, one of which is null"
| (None, None) -> print "Pair of optional types, both null"The pattern pattern₁ | pattern₂ represents the logical "or" of the two patterns pattern₁ and pattern₂. A value matches pattern₁ | pattern₂ if it matches pattern₁ or pattern₂.
Pattern clauses can make the use of guards to test predicates and variables can captured (binded in scope).
begin match token_list with
| "switch"::var::"{"::rest -> ...
| "case"::":"::var::rest when is_int var -> ...
| "case"::":"::var::rest when is_string var -> ...
| "}"::[ ] -> ...
| "}"::rest -> error "syntax error: " restMoreover, the pattern matching compiler emits a warning when a pattern is not exhaustive or some patterns are shadowed by precedent ones.
Symbolic execution
Symbolic execution is a widely used techniques in the field of computer security. It allows to analyze different execution paths of a program simultanously while tracking which inputs trigger the execution of different parts of the program. Inputs are modelled symbolically rather than taking "concrete" values. A symbolic execution engine keeps track of expressions and variables in terms of these symbolic symbols and attaches logical constraints to every branch that is being followed. Symbolic execution engines are used to track bugs by modelling the domain of all possible inputs of a program, detecting infeasible paths, dead code and proving that two code segments are equivalent.
Let's take as example this signedness bug that was found in the FreeBSD kernel and allowed, when calling the getpeername function, to read portions of kernel memory.
int compat;
{
struct file *fp;
register struct socket *so;
struct sockaddr *sa;
int len, error;
...
len = MIN(len, sa->sa_len); /* [1] */
error = copyout(sa, (caddr_t)uap->asa, (u_int)len);
if (error)
goto bad;
...
bad:
if (sa)
FREE(sa, M_SONAME);
fdrop(fp, p);
return (error);
}
The tree of the execution when the function is evaluated considering
int len our symbolic variable α, sa->sa_len as symbolic variable β
and π as the set of constraints on a symbolic variable:

We can see that at step 3 the set of possible values of the scrutinee α is bigger than the set of possible values of the input σ to the cast directive, that is: πα ⊈ πσ. For this reason the cast may fail when α is len negative number, outside the domain πσ. In C this would trigger undefined behaviour (signed overflow) that made the exploitation possible.
Every step of evaluation can be modelled as the following transition: \[ (π_{σ}, (πᵢ)ⁱ) → (π'_{σ}, (π'ᵢ)ⁱ) \] if we express the π constraints as logical formulas we can model the execution of the program in terms of Hoare Logic. State of the computation is a Hoare triple {P}C{Q} where P and Q are respectively the precondition and the postcondition that constitute the assertions of the program. C is the directive being executed. The language of the assertions P is:
| P ::= true | false | a < b | P1 ∧ P2 | P1 ∨ P2 | ¬ P |
where a and b are numbers. In the Hoare rules assertions could also take the form of
| P ::= ∀ i. P | ∃ i. P | P1 ⇒ P2 |
where i is a logical variable, but assertions of these kinds increases the complexity of the symbolic engine. Execution follows the rules of Hoare logic:
- Empty statement :
- Assignment statement : The truthness of P[a/x] is equivalent to the truth of {P} after the assignment.
- Composition : c₁ and c₂ are directives that are executed in order; {Q} is called the midcondition.
- Conditional :
- Loop : {P} is the loop invariant. After the loop is finished P holds and ¬̸b caused the loop to end.
Even if the semantics of symbolic execution engines are well defined, the user may run into different complications when applying such analysis to non trivial codebases. For example, depending on the domain, loop termination is not guaranteed. Even when termination is guaranteed, looping causes exponential branching that may lead to path explosion or state explosion. Reasoning about all possible executions of a program is not always feasible and in case of explosion usually symbolic execution engines implement heuristics to reduce the size of the search space.
Translation validation
Translators, such as translators and code generators, are huge pieces of software usually consisting of multiple subsystem and constructing an actual specification of a translator implementation for formal validation is a very long task. Moreover, different translators implement different algorithms, so the correctness proof of a translator cannot be generalized and reused to prove another translator. Translation validation is an alternative to the verification of existing translators that consists of taking the source and the target (compiled) program and proving a posteriori their semantic equivalence.
- Techniques for translation validation
- What does semantically equivalent mean
- What happens when there is no semantic equivalence
- Translation validation through symbolic execution
Translation validation of the Pattern Matching Compiler
Source program
Our algorithm takes as its input a source program and translates it into an algebraic data structure which type we call decision_tree.
type decision_tree =
| Unreachable
| Failure
| Leaf of source_expr
| Guard of source_blackbox * decision_tree * decision_tree
| Switch of accessor * (constructor * decision_tree) list * decision_treeUnreachable, Leaf of source_expr and Failure are the terminals of the three. We distinguish
- Unreachable: statically it is known that no value can go there
- Failure: a value matching this part results in an error
- Leaf: a value matching this part results into the evaluation of a source black box of code
Our algorithm doesn't support type-declaration-based analysis to know the list of constructors at a given type. Let's consider some trivial examples:
| function true -> 1 |
is translated to
| Switch ([(true, Leaf 1)], Failure) |
while
| function |
| | true -> 1 |
| | false -> 2 |
will be translated to
| Switch ([(true, Leaf 1); (false, Leaf 2)]) |
It is possible to produce Unreachable examples by using refutation clauses (a "dot" in the right-hand-side)
| | true -> 1 |
| | false -> 2 |
| | _ -> . |
that gets translated into
| Switch ([(true, Leaf 1); (false, Leaf 2)], Unreachable) |
We trust this annotation, which is reasonable as the type-checker verifies that it indeed holds.
Guard nodes of the tree are emitted whenever a guard is found. Guards node contains a blackbox of code that is never evaluated and two branches, one that is taken in case the guard evaluates to true and the other one that contains the path taken when the guard evaluates to true.
\begin{comment} [ ] Finisci con Switch [ ] Spiega del fallback \end{comment}The source code of a pattern matching function has the following form:
| match variable with |
| | pattern₁ → expr₁ |
| | pattern₂ when guard → expr₂ |
| | pattern₃ as var → expr₃ |
| ⋮ |
| | pₙ → exprₙ |
Patterns could or could not be exhaustive.
Pattern matching code could also be written using the more compact form:
| | pattern₁ → expr₁ |
| | pattern₂ when guard → expr₂ |
| | pattern₃ as var → expr₃ |
| ⋮ |
| | pₙ → exprₙ |
This BNF grammar describes formally the grammar of the source program:
| start ::= "match" id "with" patterns | "function" patterns |
| patterns ::= (pattern0|pattern1) pattern1+ |
| ;; pattern0 and pattern1 are needed to distinguish the first case in which |
| ;; we can avoid writing the optional vertical line |
| pattern0 ::= clause |
| pattern1 ::= "|" clause |
| clause ::= lexpr "->" rexpr |
| lexpr ::= rule (ε|condition) |
| rexpr ::= _code ;; arbitrary code |
| rule ::= wildcard|variable|constructor_pattern| or_pattern ;; |
| wildcard ::= "_" |
| variable ::= identifier |
| constructor_pattern ::= constructor (rule|ε) (assignment|ε) |
| constructor ::= int|float|char|string|bool |unit|record|exn|objects|ref |list|tuple|array|variant|parameterized_variant ;; data types |
| or_pattern ::= rule ("|" wildcard|variable|constructor_pattern)+ |
| condition ::= "when" bexpr |
| assignment ::= "as" id |
| bexpr ::= _code ;; arbitrary code |
The source program is parsed using the ocaml-compiler-libs library. The result of parsing, when successful, results in a list of clauses and a list of type declarations. Every clause consists of three objects: a left-hand-side that is the kind of pattern expressed, an option guard and a right-hand-side expression. Patterns are encoded in the following way:
| pattern | type |
|---|---|
| _ | Wildcard |
| p₁ as x | Assignment |
| c(p₁,p₂,…,pₙ) | Constructor |
| (p₁| p₂) | Orpat |
Once parsed, the type declarations and the list of clauses are encoded in the form of a matrix that is later evaluated using a matrix decomposition algorithm.
Patterns are of the form
| pattern | type of pattern |
|---|---|
| _ | wildcard |
| x | variable |
| c(p₁,p₂,…,pₙ) | constructor pattern |
| (p₁| p₂) | or-pattern |
The pattern p matches a value v, written as p ≼ v, when one of the following rules apply
| _ | ≼ | v | ∀v |
| x | ≼ | v | ∀v |
| (p₁ | p₂) | ≼ | v | iff p₁ ≼ v or p₂ ≼ v |
| c(p₁, p₂, …, pₐ) | ≼ | c(v₁, v₂, …, vₐ) | iff (p₁, p₂, …, pₐ) ≼ (v₁, v₂, …, vₐ) |
| (p₁, p₂, …, pₐ) | ≼ | (v₁, v₂, …, vₐ) | iff pᵢ ≼ vᵢ ∀i ∈ [1..a] |
When a value v matches pattern p we say that v is an instance of p.
During compilation by the translators, expressions at the right-hand-side are compiled into Lambda code and are referred as lambda code actions lᵢ.
We define the pattern matrix P as the matrix |m x n| where m bigger or equal than the number of clauses in the source program and n is equal to the arity of the constructor with the gratest arity.
\begin{equation*} P = \begin{pmatrix} p_{1,1} & p_{1,2} & \cdots & p_{1,n} \\ p_{2,1} & p_{2,2} & \cdots & p_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ p_{m,1} & p_{m,2} & \cdots & p_{m,n} ) \end{pmatrix} \end{equation*}every row of P is called a pattern vector $\vec{p_i}$ = (p₁, p₂, …, pₙ); In every instance of P pattern vectors appear normalized on the length of the longest pattern vector. Considering the pattern matrix P we say that the value vector $\vec{v}$ = (v₁, v₂, …, vᵢ) matches the pattern vector pᵢ in P if and only if the following two conditions are satisfied:
- pi,1, pi,2, ⋯, pi,n ≼ (v₁, v₂, …, vᵢ)
- ∀j < i pj,1, pj,2, ⋯, pj,n ⋠ (v₁, v₂, …, vᵢ)
We can define the following three relations with respect to patterns:
- Pattern p is less precise than pattern q, written p ≼ q, when all instances of q are instances of p
- Pattern p and q are equivalent, written p ≡ q, when their instances are the same
- Patterns p and q are compatible when they share a common instance
Wit the support of two auxiliary functions
-
tail of an ordered family
tail((xᵢ)i ∈ I) := (xᵢ)i ≠ min(I) -
first non-⊥ element of an ordered family
First((xᵢ)ⁱ) := ⊥ \quad \quad \quad if ∀i, xᵢ = ⊥ First((xᵢ)ⁱ) := x_min{i | xᵢ ≠ ⊥} \quad if ∃i, xᵢ ≠ ⊥
we now define what it means to run a pattern row against a value vector of the same length, that is (pᵢ)ⁱ(vᵢ)ⁱ
| pᵢ | vᵢ | resultpat |
|---|---|---|
| ∅ | (∅) | [] |
| (_, tail(pᵢ)ⁱ) | (vᵢ) | tail(pᵢ)ⁱ(tail(vᵢ)ⁱ) |
| (x, tail(pᵢ)ⁱ) | (vᵢ) | σ[x↦v₀] if tail(pᵢ)ⁱ(tail(vᵢ)ⁱ) = σ |
| (K(qⱼ)ʲ, tail(pᵢ)ⁱ) | (K(v'ⱼ)ʲ,tail(vⱼ)ʲ) | ((qⱼ)ʲ |
| (K(qⱼ)ʲ, tail(pᵢ)ⁱ) | (K'(v'ₗ)ˡ,tail(vⱼ)ʲ) | ⊥ if K ≠ K' |
| (q₁|q₂, tail(pᵢ)ⁱ) | (vᵢ)ⁱ | First((q₁,tail(pᵢ)ⁱ)(vᵢ)ⁱ, (q₂,tail(pᵢ)ⁱ)(vᵢ)ⁱ) |
A source program tₛ is a collection of pattern clauses pointing to bb terms. Running a program tₛ against an input value vₛ, written tₛ(vₛ) produces a result r belonging to the following grammar:
| tₛ ::= (p → bb)i∈I |
| tₛ(vₛ) → r |
| r ::= guard list * (Match (σ, bb) | NoMatch | Absurd) |
We can define what it means to run an input value vₛ against a source program tₛ:
| First((xᵢ)ⁱ) := x_min{i | xᵢ ≠ ⊥} \quad if ∃i, xᵢ ≠ ⊥ |
| tₛ(vₛ) := NoMatch \quad if ∀i, pᵢ(vₛ) = ⊥ |
| tₛ(vₛ) = { Absurd if bbi₀ = . (refutation clause) |
| \quad \quad \quad \quad \quad Match (σ, bbi₀) otherwise |
| \quad \quad \quad \quad \quad where iₒ = min{i | pᵢ(vₛ) ≠ ⊥} |
guard and bb expressions are treated as blackboxes of OCaml code. A sound approach for treating these blackboxes would be to inspect the OCaml compiler during translation to Lambda code and extract the blackboxes compiled in their Lambda representation. This would allow to test for equality with the respective blackbox at the target level. Given that this level of introspection is currently not possibile, we decided to restrict the structure of blackboxes to the following (valid) OCaml code:
external guard : 'a -> 'b = "guard"
external observe : 'a -> 'b = "observe"We assume these two external functions guard and observe with a valid type that lets the user pass any number of arguments to them. All the guards are of the form \texttt{guard <arg> <arg> <arg>}, where the <arg> are expressed using the OCaml pattern matching language. Similarly, all the right-hand-side expressions are of the form \texttt{observe <arg> <arg> …} with the same constraints on arguments.
(* declaration of an algebraic and recursive datatype t *)
type t = K1 | K2 of t
let _ = function
| K1 -> observe 0
| K2 K1 -> observe 1
| K2 x when guard x -> observe 2 (* guard inspects the x variable *)
| K2 (K2 x) as y when guard x y -> observe 3
| K2 _ -> observe 4We note that the right hand side of observe is just an arbitrary value and in this case just enumerates the order in which expressions appear. Even if this is an oversimplification of the problem for the prototype, it must be noted that at the compiler level we have the possibility to compile the pattern clauses in two separate steps so that the guards and right-hand-side expressions are semantically equal to their counterparts at the target program level.
\begin{lstlisting} let _ = function | K1 -> lambda₀ | K2 K1 -> lambda₁ | K2 x when lambda-guard₀ -> lambda₂ | K2 (K2 x) as y when lambda-guard₁ -> lambda₃ | K2 _ -> lambda₄ \end{lstlisting}⊂subsection{Matrix decomposition of pattern clauses} We define a new object, the clause matrix P → L of size |m x n+1| that associates pattern vectors $\vec{p_i}$ to lambda code action lᵢ.
\begin{equation*} P → L = \begin{pmatrix} p_{1,1} & p_{1,2} & \cdots & p_{1,n} → l₁ \\ p_{2,1} & p_{2,2} & \cdots & p_{2,n} → l₂ \\ \vdots & \vdots & \ddots & \vdots → \vdots \\ p_{m,1} & p_{m,2} & \cdots & p_{m,n} → lₘ \end{pmatrix} \end{equation*}The initial input of the decomposition algorithm C consists of a vector of variables $\vec{x}$ = (x₁, x₂, …, xₙ) of size n where n is the arity of the type of x and the clause matrix P → L. That is:
\begin{equation*} C((\vec{x} = (x₁, x₂, ..., xₙ), \begin{pmatrix} p_{1,1} & p_{1,2} & \cdots & p_{1,n} → l₁ \\ p_{2,1} & p_{2,2} & \cdots & p_{2,n} → l₂ \\ \vdots & \vdots & \ddots & \vdots → \vdots \\ p_{m,1} & p_{m,2} & \cdots & p_{m,n} → lₘ \end{pmatrix}) \end{equation*}The base case C₀ of the algorithm is the case in which the $\vec{x}$ is an empty sequence and the result of the compilation C₀ is l₁
\begin{equation*} C₀((), \begin{pmatrix} → l₁ \\ → l₂ \\ → \vdots \\ → lₘ \end{pmatrix}) = l₁ \end{equation*}When $\vec{x}$ ≠ () then the compilation advances using one of the following four rules:
-
Variable rule: if all patterns of the first column of P are wildcard patterns or bind the value to a variable, then
\begin{equation*} C(\vec{x}, P → L) = C((x₂, x₃, ..., xₙ), P' → L') \end{equation*}where
\begin{equation*} \begin{pmatrix} p_{1,2} & \cdots & p_{1,n} & → & (let & y₁ & x₁) & l₁ \\ p_{2,2} & \cdots & p_{2,n} & → & (let & y₂ & x₁) & l₂ \\ \vdots & \ddots & \vdots & → & \vdots & \vdots & \vdots & \vdots \\ p_{m,2} & \cdots & p_{m,n} & → & (let & yₘ & x₁) & lₘ \end{pmatrix} \end{equation*}That means in every lambda action lᵢ there is a binding of x₁ to the variable that appears on the pattern pi,1. Bindings are omitted for wildcard patterns and the lambda action lᵢ remains unchanged.
- Constructor rule: if all patterns in the first column of P are constructors patterns of the form k(q₁, q₂, …, qn') we define a new matrix, the specialized clause matrix S, by applying the following transformation on every row p: \begin{lstlisting}[mathescape,columns=fullflexible,basicstyle=\fontfamily{lmvtt}\selectfont,] for every c ∈ Set of constructors for i ← 1 .. m let kᵢ ← constructor_of($p_{i,1}$) if kᵢ = c then p ← $q_{i,1}$, $q_{i,2}$, …, $q_{i,n'}$, $p_{i,2}$, $p_{i,3}$, …, $p_{i, n}$ \end{lstlisting} Patterns of the form $q_{i,j}$ matches on the values of the constructor and we define new fresh variables y₁, y₂, …, yₐ so that the lambda action lᵢ becomes \begin{lstlisting}[mathescape,columns=fullflexible,basicstyle=\fontfamily{lmvtt}\selectfont,] (let (y₁ (field 0 x₁)) (y₂ (field 1 x₁)) … (yₐ (field (a-1) x₁)) lᵢ) \end{lstlisting} and the result of the compilation for the set of constructors {c₁, c₂, …, cₖ} is: \begin{lstlisting}[mathescape,columns=fullflexible,basicstyle=\fontfamily{lmvtt}\selectfont,] switch x₁ with case c₁: l₁ case c₂: l₂ … case cₖ: lₖ default: exit \end{lstlisting}
-
Orpat rule: there are various strategies for dealing with or-patterns. The most naive one is to split the or-patterns. For example a row p containing an or-pattern:
\begin{equation*} (p_{i,1}|q_{i,1}|r_{i,1}), p_{i,2}, ..., p_{i,m} → lᵢ \end{equation*}results in three rows added to the clause matrix
\begin{equation*} p_{i,1}, p_{i,2}, ..., p_{i,m} → lᵢ \\ \end{equation*} \begin{equation*} q_{i,1}, p_{i,2}, ..., p_{i,m} → lᵢ \\ \end{equation*} \begin{equation*} r_{i,1}, p_{i,2}, ..., p_{i,m} → lᵢ \end{equation*} - Mixture rule: When none of the previous rules apply the clause matrix P → L is split into two clause matrices, the first P₁ → L₁ that is the largest prefix matrix for which one of the three previous rules apply, and P₂ → L₂ containing the remaining rows. The algorithm is applied to both matrices.
It is important to note that the application of the decomposition algorithm converges. This intuition can be verified by defining the size of the clause matrix P → L as equal to the length of the longest pattern vector $\vec{p_i}$ and the length of a pattern vector as the number of symbols that appear in the clause. While it is very easy to see that the application of rules 1) and 4) produces new matrices of length equal or smaller than the original clause matrix, we can show that:
-
with the application of the constructor rule the pattern vector $\vec{p_i}$ loses one symbol after its decomposition:
|(pi,1 (q₁, q₂, …, qn'), pi,2, pi,3, …, pi,n)| = n + n' |(qi,1, qi,2, …, qi,n', pi,2, pi,3, …, pi,n)| = n + n' - 1 - with the application of the orpat rule, we add one row to the clause matrix P → L but the length of a row containing an Or-pattern decreases
In our prototype we make use of accessors to encode stored values.
\begin{minipage}{0.6\linewidth}
\begin{verbatim} let value = 1 :: 2 :: 3 :: [] (* that can also be written *) let value = [] |> List.cons 3 |> List.cons 2 |> List.cons 1 \end{verbatim}\end{minipage} \hfill \begin{minipage}{0.5\linewidth}
\begin{verbatim} (field 0 x) = 1 (field 0 (field 1 x)) = 2 (field 0 (field 1 (field 1 x)) = 3 (field 0 (field 1 (field 1 (field 1 x)) = [] \end{verbatim}\end{minipage} An \emph{accessor} a represents the access path to a value that can be reached by deconstructing the scrutinee.
| a ::= Here | n.a |
The above example, in encoded form:
\begin{verbatim} Here = 1 1.Here = 2 1.1.Here = 3 1.1.1.Here = [] \end{verbatim}In our prototype the source matrix mₛ is defined as follows
| SMatrix mₛ := (aⱼ)j∈J, ((pij)j∈J → bbᵢ)i∈I |
Source matrices are used to build source decision trees Cₛ. A decision tree is defined as either a Leaf, a Failure terminal or an intermediate node with different children sharing the same accessor a and an optional fallback. Failure is emitted only when the patterns don't cover the whole set of possible input values S. The fallback is not needed when the user doesn't use a wildcard pattern. %%% Give example of thing
| Cₛ ::= Leaf bb | Switch(a, (Kᵢ → Cᵢ)i∈S , C?) | Failure | Unreachable |
| vₛ ::= K(vᵢ)i∈I | n ∈ ℕ |
We say that a translation of a source program to a decision tree is correct when for every possible input, the source program and its respective decision tree produces the same result
| ∀vₛ, tₛ(vₛ) = 〚tₛ〛ₛ(vₛ) |
We define the decision tree of source programs 〚tₛ〛 in terms of the decision tree of pattern matrices 〚mₛ〛 by the following:
| 〚((pᵢ → bbᵢ)i∈I〛 := 〚(Here), (pᵢ → bbᵢ)i∈I 〛 |
Decision tree computed from pattern matrices respect the following invariant:
| ∀v (vᵢ)i∈I = v(aᵢ)i∈I → 〚m〛(v) = m(vᵢ)i∈I for m = ((aᵢ)i∈I, (rᵢ)i∈I) |
| v(Here) = v |
| K(vᵢ)ⁱ(k.a) = vₖ(a) if k ∈ [0;n[ |
We proceed to show the correctness of the invariant by a case analysys.
Base cases:
- [| ∅, (∅ → bbᵢ)ⁱ |] ≡ Leaf bbᵢ where i := min(I), that is a decision tree [|ms|] defined by an empty accessor and empty patterns pointing to blackboxes bbᵢ. This respects the invariant because a source matrix in the case of empty rows returns the first expression and (Leaf bb)(v) := Match bb
- [| (aⱼ)ʲ, ∅ |] ≡ Failure
Regarding non base cases: Let's first define some auxiliary functions
-
The index family of a constructor
Idx(K) := [0; arity(K)[ -
head of an ordered family (we write x for any object here, value, pattern etc.)
head((xᵢ)i ∈ I) = x_min(I) -
tail of an ordered family
tail((xᵢ)i ∈ I) := (xᵢ)i ≠ min(I) -
head constructor of a value or pattern
constr(K(xᵢ)ⁱ) = K constr(_) = ⊥ constr(x) = ⊥ -
first non-⊥ element of an ordered family
First((xᵢ)ⁱ) := ⊥ \quad \quad \quad if ∀i, xᵢ = ⊥ First((xᵢ)ⁱ) := x_min{i | xᵢ ≠ ⊥} \quad if ∃i, xᵢ ≠ ⊥ - definition of group decomposition:
| let constrs((pᵢ)i ∈ I) = { K | K = constr(pᵢ), i ∈ I } |
| let Groups(m) where m = ((aᵢ)ⁱ ((pᵢⱼ)ⁱ → eⱼ)ⁱʲ) = |
| \quad \quad let (Kₖ)ᵏ = constrs(pᵢ₀)ⁱ in |
| \quad \quad ( Kₖ → |
| \quad \quad \quad \quad ((a₀.ₗ)ˡ |
| \quad \quad \quad \quad ( |
| \quad \quad \quad \quad if pₒⱼ is Kₖ(qₗ) then |
| \quad \quad \quad \quad \quad \quad (qₗ)ˡ |
| \quad \quad \quad \quad if pₒⱼ is _ then |
| \quad \quad \quad \quad \quad \quad (_)ˡ |
| \quad \quad \quad \quad else ⊥ |
| \quad \quad \quad \quad )ʲ |
| \quad \quad ), ( |
| \quad \quad \quad \quad tail(aᵢ)ⁱ, (tail(pᵢⱼ)ⁱ → eⱼ if p₀ⱼ is _ else ⊥)ʲ |
| \quad \quad ) |
Groups(m) is an auxiliary function that decomposes a matrix m into submatrices, according to the head constructor of their first pattern. Groups(m) returns one submatrix m_r for each head constructor K that occurs on the first row of m, plus one "wildcard submatrix" mwild that matches on all values that do not start with one of those head constructors. Intuitively, m is equivalent to its decomposition in the following sense: if the first pattern of an input vector (v_i)^i starts with one of the head constructors Kₖ, then running (v_i)^i against m is the same as running it against the submatrix mKₖ; otherwise (its head constructor ∉ (Kₖ)ᵏ) it is equivalent to running it against the wildcard submatrix.
We formalize this intuition as follows
Lemma (Groups):
Let m be a matrix with
| Groups(m) = (kᵣ → mᵣ)^k, mwild |
For any value vector $(v_i)^l$ such that $v_0 = k(v'_l)^l$ for some constructor k, we have:
| if k = kₖ \text{ for some k then} |
| \quad m(vᵢ)ⁱ = mₖ((vl')ˡ |
| \text{else} |
| \quad m(vᵢ)ⁱ = mwild(vᵢ)i∈I\DZ |
Proof:
Let m be a matrix ((aᵢ)ⁱ, ((pᵢⱼ)ⁱ → eⱼ)ʲ) with
| Groups(m) = (Kₖ → mₖ)ᵏ, mwild |
Below we are going to assume that m is a simplified matrix such that the first row does not contain an or-pattern or a binding to a variable.
Let (vᵢ)ⁱ be an input matrix with v₀ = Kᵥ(v'l)ˡ for some constructor Kᵥ. We have to show that:
-
if Kₖ = Kᵥ for some Kₖ ∈ constrs(p₀ⱼ)ʲ, then
m(vᵢ)ⁱ = mₖ((v'ₗ)ˡ +tail(vᵢ)ⁱ) - otherwise m(vᵢ)ⁱ = mwild(tail(vᵢ)ⁱ)
Let us call (rₖⱼ) the j-th row of the submatrix mₖ, and rⱼwild the j-th row of the wildcard submatrix mwild.
Our goal contains same-behavior equalities between matrices, for a fixed input vector (vᵢ)ⁱ. It suffices to show same-behavior equalities between each row of the matrices for this input vector. We show that for any j,
-
if Kₖ = Kᵥ for some Kₖ ∈ constrs(p₀ⱼ)ʲ, then
(pᵢⱼ)ⁱ(vᵢ)ⁱ = rₖⱼ((v'ₗ)ˡ +tail(vᵢ)ⁱ -
otherwise
(pᵢⱼ)ⁱ(vᵢ)ⁱ = rⱼwild tail(vᵢ)ⁱ
In the first case (Kᵥ is Kₖ for some Kₖ ∈ constrs(p₀ⱼ)ʲ), we have to prove that
| (pᵢⱼ)ⁱ(vᵢ)ⁱ = rₖⱼ((v'ₗ)ˡ |
By definition of mₖ we know that rₖⱼ is equal to
| if pₒⱼ is Kₖ(qₗ) then |
| \quad (qₗ)ˡ |
| if pₒⱼ is _ then |
| \quad (_)ˡ |
| else ⊥ |
By definition of (pᵢ)ⁱ(vᵢ)ⁱ we know that (pᵢⱼ)ⁱ(vᵢ) is equal to
| (K(qⱼ)ʲ, tail(pᵢⱼ)ⁱ) (K(v'ₗ)ˡ,tail(vᵢ)ⁱ) := ((qⱼ)ʲ |
| (_, tail(pᵢⱼ)ⁱ) (vᵢ) := tail(pᵢⱼ)ⁱ(tail(vᵢ)ⁱ) |
| (K(qⱼ)ʲ, tail(pᵢⱼ)ⁱ) (K'(v'ₗ)ˡ,tail(vⱼ)ʲ) := ⊥ if K ≠ K' |
We prove this first case by a second case analysis on p₀ⱼ.
TODO
\begin{comment} GOAL: | (pᵢⱼ)ⁱ(vᵢ)ⁱ = rₖⱼ((v'ₗ)ˡ +++ tail(vᵢ)ⁱ case analysis on pₒⱼ: | pₒⱼ | pᵢⱼ | |--------+-----------------------| | Kₖ(qₗ) | (qₗ)ˡ +++ tail(pᵢⱼ)ⁱ | | else | ⊥ | that is exactly the same as rₖⱼ := (qₗ)ˡ +++ tail(pᵢⱼ)ⁱ → eⱼ But I am just putting together the definition given above (in the pdf). Second case, below: the wildcard matrix r_{jwild} is | tail(aᵢ)ⁱ, (tail(pᵢⱼ)ⁱ → eⱼ if p₀ⱼ is _ else ⊥)ʲ case analysis on p₀ⱼ: | pₒⱼ | (pᵢⱼ)ⁱ | |--------+-----------------------| | Kₖ(qₗ) | (qₗ)ˡ +++ tail(pᵢⱼ)ⁱ | not possible because we are in the second case | _ | (_)ˡ +++ tail(pᵢⱼ)ⁱ | | else | ⊥ | Both seems too trivial to be correct. \end{comment}In the second case (Kᵥ is distinct from Kₖ for all Kₖ ∈ constrs(pₒⱼ)ʲ), we have to prove that
| (pᵢⱼ)ⁱ(vᵢ)ⁱ = rⱼwild tail(vᵢ)ⁱ |
TODO
Target translation
The target program of the following general form is parsed using a parser generated by Menhir, a LR(1) parser generator for the OCaml programming language. Menhir compiles LR(1) a grammar specification, in this case a subset of the Lambda intermediate language, down to OCaml code. This is the grammar of the target language (TODO: check menhir grammar)
| start ::= sexpr |
| sexpr ::= variable | string | "(" special_form ")" |
| string ::= "\"" identifier "\"" ;; string between doublequotes |
| variable ::= identifier |
| special_form ::= let|catch|if|switch|switch-star|field|apply|isout |
| let ::= "let" assignment sexpr ;; (assignment sexpr)+ outside of pattern match code |
| assignment ::= "function" variable variable+ ;; the first variable is the identifier of the function |
| field ::= "field" digit variable |
| apply ::= ocaml_lambda_code ;; arbitrary code |
| catch ::= "catch" sexpr with sexpr |
| with ::= "with" "(" label ")" |
| exit ::= "exit" label |
| switch-star ::= "switch*" variable case* |
| switch::= "switch" variable case* "default:" sexpr |
| case ::= "case" casevar ":" sexpr |
| casevar ::= ("tag"|"int") integer |
| if ::= "if" bexpr sexpr sexpr |
bexpr ::= "(" ("!="|"="\vert{}">"|"<="|">"|"<") sexpr digit | field ")" |
| label ::= integer |
The prototype doesn't support strings.
The AST built by the parser is traversed and evaluated by the symbolic execution engine. Given that the target language supports jumps in the form of "catch - exit" blocks the engine tries to evaluate the instructions inside the blocks and stores the result of the partial evaluation into a record. When a jump is encountered, the information at the point allows to finalize the evaluation of the jump block. In the environment the engine also stores bindings to values and functions. Integer additions and subtractions are simplified in a second pass. The result of the symbolic evaluation is a target decision tree Cₜ
| Cₜ ::= Leaf bb | Switch(a, (πᵢ → Cᵢ)i∈S , C?) | Failure |
| vₜ ::= Cell(tag ∈ ℕ, (vᵢ)i∈I) | n ∈ ℕ |
Every branch of the decision tree is "constrained" by a domain
| Domain π = { n|n∈ℕ x n|n∈Tag⊆ℕ } |
Intuitively, the π condition at every branch tells us the set of possible values that can "flow" through that path. π conditions are refined by the engine during the evaluation; at the root of the decision tree the domain corresponds to the set of possible values that the type of the function can hold. C? is the fallback node of the tree that is taken whenever the value at that point of the execution can't flow to any other subbranch. Intuitively, the πfallback condition of the C? fallback node is
| πfallback = ¬\bigcuplimitsi∈Iπᵢ |
The fallback node can be omitted in the case where the domain of the children nodes correspond to set of possible values pointed by the accessor at that point of the execution
| domain(vₛ(a)) = \bigcuplimitsi∈Iπᵢ |
We say that a translation of a target program to a decision tree is correct when for every possible input, the target program and its respective decision tree produces the same result
| ∀vₜ, tₜ(vₜ) = 〚tₜ〛ₜ(vₜ) |
Equivalence checking
The equivalence checking algorithm takes as input a domain of possible values \emph{S} and a pair of source and target decision trees and in case the two trees are not equivalent it returns a counter example. Our algorithm respects the following correctness statement:
\begin{comment} TODO: we have to define what \coversTEX mean for readers to understand the specifications (or we use a simplifying lie by hiding \coversTEX in the statements). \end{comment} \begin{align*} \EquivTEX S {C_S} {C_T} \emptyqueue = \YesTEX \;\land\; \coversTEX {C_T} S & \implies \forall v_S \approx v_T \in S,\; C_S(v_S) = C_T(v_T) \\ \EquivTEX S {C_S} {C_T} \emptyqueue = \NoTEX {v_S} {v_T} \;\land\; \coversTEX {C_T} S & \implies v_S \approx v_T \in S \;\land\; C_S(v_S) \neq C_T(v_T) \end{align*}Our equivalence-checking algorithm $\EquivTEX S {C_S} {C_T} G$ is a exactly decision procedure for the provability of the judgment $(\EquivTEX S {C_S} {C_T} G)$, defined below.
\begin{mathpar} \begin{array}{l@{~}r@{~}l} & & \text{\emph{constraint trees}} \\ C & \bnfeq & \Leaf t \\ & \bnfor & \Failure \\ & \bnfor & \Switch a {\Fam i {\pi_i, C_i}} \Cfb \\ & \bnfor & \Guard t {C_0} {C_1} \\ \end{array} \begin{array}{l@{~}r@{~}l} & & \text{\emph{boolean result}} \\ b & \in & \{ 0, 1 \} \\[0.5em] & & \text{\emph{guard queues}} \\ G & \bnfeq & (t_1 = b_1), \dots, (t_n = b_n) \\ \end{array} \begin{array}{l@{~}r@{~}l} & & \text{\emph{input space}} \\ S & \subseteq & \{ (v_S, v_T) \mid \vrel {v_S} {v_T} \} \\ \end{array} \\ \infer{ } {\EquivTEX \emptyset {C_S} {C_T} G} \infer{ } {\EquivTEX S \Failure \Failure \emptyqueue} \infer {\trel {t_S} {t_T}} {\EquivTEX S {\Leaf {t_S}} {\Leaf {t_T}} \emptyqueue} \infer {\forall i,\; \EquivTEX {(S \land a = K_i)} {C_i} {\trim {C_T} {a = K_i}} G \\ \EquivTEX {(S \land a \notin \Fam i {K_i})} \Cfb {\trim {C_T} {a \notin \Fam i {K_i}}} G } {\EquivTEX S {\Switch a {\Fam i {K_i, C_i}} \Cfb} {C_T} G} \begin{comment} % TODO explain somewhere why the judgment is not symmetric: % we avoid defining trimming on source trees, which would % require more expressive conditions than just constructors \end{comment} \infer {C_S \in {\Leaf t, \Failure} \\ \forall i,\; \EquivTEX {(S \land a \in D_i)} {C_S} {C_i} G \\ \EquivTEX {(S \land a \notin \Fam i {D_i})} {C_S} \Cfb G} {\EquivTEX S {C_S} {\Switch a {\Fam i {D_i} {C_i}} \Cfb} G} \infer {\EquivTEX S {C_0} {C_T} {G, (t_S = 0)} \\ \EquivTEX S {C_1} {C_T} {G, (t_S = 1)}} {\EquivTEX S {\Guard {t_S} {C_0} {C_1}} {C_T} G} \infer {\trel {t_S} {t_T} \\ \EquivTEX S {C_S} {C_b} G} {\EquivTEX S {C_S} {\Guard {t_T} {C_0} {C_1}} {(t_S = b), G}} \end{mathpar}Running a program tₛ or its translation 〚tₛ〛 against an input vₛ produces as a result r in the following way:
| ( 〚tₛ〛ₛ(vₛ) ≡ Cₛ(vₛ) ) → r |
| tₛ(vₛ) → r |
Likewise
| ( 〚tₜ〛ₜ(vₜ) ≡ Cₜ(vₜ) ) → r |
| tₜ(vₜ) → r |
| result r ::= guard list * (Match blackbox | NoMatch | Absurd) |
| guard ::= blackbox. |
Having defined equivalence between two inputs of which one is expressed in the source language and the other in the target language, vₛ ≃ vₜ, we can define the equivalence between a couple of programs or a couple of decision trees
| tₛ ≃ tₜ := ∀vₛ≃vₜ, tₛ(vₛ) = tₜ(vₜ) |
| Cₛ ≃ Cₜ := ∀vₛ≃vₜ, Cₛ(vₛ) = Cₜ(vₜ) |
The result of the proposed equivalence algorithm is Yes or No(vₛ, vₜ). In particular, in the negative case, vₛ and vₜ are a couple of possible counter examples for which the decision trees produce a different result.
In the presence of guards we can say that two results are equivalent modulo the guards queue, written r₁ ≃gs r₂, when:
| (gs₁, r₁) ≃gs (gs₂, r₂) ⇔ (gs₁, r₁) = (gs₂ ++ gs, r₂) |
We say that Cₜ covers the input space S, written covers(Cₜ, S) when every value vₛ∈S is a valid input to the decision tree Cₜ. (TODO: rephrase) Given an input space S and a couple of decision trees, where the target decision tree Cₜ covers the input space S we can define equivalence:
| equiv(S, Cₛ, Cₜ, gs) = Yes ∧ covers(Cₜ, S) → ∀vₛ≃vₜ ∈ S, Cₛ(vₛ) ≃gs Cₜ(vₜ) |
Similarly we say that a couple of decision trees in the presence of an input space S are not equivalent in the following way:
| equiv(S, Cₛ, Cₜ, gs) = No(vₛ,vₜ) ∧ covers(Cₜ, S) → vₛ≃vₜ ∈ S ∧ Cₛ(vₛ) ≠gs Cₜ(vₜ) |
Corollary: For a full input space S, that is the universe of the target program:
| equiv(S, 〚tₛ〛ₛ, 〚tₜ〛ₜ, ∅) = Yes ⇔ tₛ ≃ tₜ |
⊂subsection{The trimming lemma} The trimming lemma allows to reduce the size of a decision tree given an accessor a → π relation (TODO: expand)
| ∀vₜ ∈ (a→π), Cₜ(vₜ) = Ct/a→π(vₜ) |
We prove this by induction on Cₜ:
-
Cₜ = Leafbb: when the decision tree is a leaf terminal, the result of trimming on a Leaf is the Leaf itself
Leafbb/a→π(v) = Leafbb(v) -
The same applies to Failure terminal
Failure/a→π(v) = Failure(v) -
When Cₜ = Switch(b, (π→Cᵢ)ⁱ)/a→π then we look at the accessor a of the subtree Cᵢ and we define πᵢ' = πᵢ if a≠b else πᵢ∩π Trimming a switch node yields the following result:
Switch(b, (π→Cᵢ)i∈I)/a→π := Switch(b, (π'ᵢ→Ci/a→π)i∈I)
For the trimming lemma we have to prove that running the value vₜ against the decision tree Cₜ is the same as running vₜ against the tree Ctrim that is the result of the trimming operation on Cₜ
| Cₜ(vₜ) = Ctrim(vₜ) = Switch(b, (πᵢ'→Ci/a→π)i∈I)(vₜ) |
We can reason by first noting that when vₜ∉(b→πᵢ)ⁱ the node must be a Failure node. In the case where ∃k | vₜ∈(b→πₖ) then we can prove that
| Ck/a→π(vₜ) = Switch(b, (πᵢ'→Ci/a→π)i∈I)(vₜ) |
because when a ≠ b then πₖ'= πₖ and this means that vₜ∈πₖ' while when a = b then πₖ'=(πₖ∩π) and vₜ∈πₖ' because:
- by the hypothesis, vₜ∈π
- we are in the case where vₜ∈πₖ
So vₜ ∈ πₖ' and by induction
| Cₖ(vₜ) = Ck/a→π(vₜ) |
We also know that ∀vₜ∈(b→πₖ) → Cₜ(vₜ) = Cₖ(vₜ) By putting together the last two steps, we have proven the trimming lemma.
\begin{comment} TODO: what should I say about covering??? I swap π and π' Covering lemma: ∀a,π covers(Cₜ,S) → covers(C_{t/a→π}, (S∩a→π)) Uᵢπⁱ ≈ Uᵢπ'∩(a→π) ≈ (Uᵢπ')∩(a→π) %% %%%%%%% Also: Should I swap π and π' ? \end{comment}⊂subsection{Equivalence checking} The equivalence checking algorithm takes as parameters an input space S, a source decision tree Cₛ and a target decision tree Cₜ:
| equiv(S, Cₛ, Cₜ) → Yes | No(vₛ, vₜ) |
When the algorithm returns Yes and the input space is covered by Cₛ we can say that the couple of decision trees are the same for every couple of source value vₛ and target value vₜ that are equivalent.
\begin{comment} Define "covered" Is it correct to say the same? How to correctly distinguish in words ≃ and = ? \end{comment}| equiv(S, Cₛ, Cₜ) = Yes and cover(Cₜ, S) → ∀ vₛ ≃ vₜ∈S ∧ Cₛ(vₛ) = Cₜ(vₜ) |
In the case where the algorithm returns No we have at least a couple of counter example values vₛ and vₜ for which the two decision trees outputs a different result.
| equiv(S, Cₛ, Cₜ) = No(vₛ,vₜ) and cover(Cₜ, S) → ∀ vₛ ≃ vₜ∈S ∧ Cₛ(vₛ) ≠ Cₜ(vₜ) |
We define the following
| Forall(Yes) = Yes |
| Forall(Yes::l) = Forall(l) |
| Forall(No(vₛ,vₜ)::_) = No(vₛ,vₜ) |
There exists and are injective:
| int(k) ∈ ℕ (arity(k) = 0) |
| tag(k) ∈ ℕ (arity(k) > 0) |
| π(k) = {n| int(k) = n} x {n| tag(k) = n} |
where k is a constructor.
\begin{comment} TODO: explain: ∀v∈a→π, C_{/a→π}(v) = C(v) \end{comment}We proceed by case analysis:
\begin{comment} I start numbering from zero to leave the numbers as they were on the blackboard, were we skipped some things I think the unreachable case should go at the end. \end{comment}- in case of unreachable:
| Cₛ(vₛ) = Absurd(Unreachable) ≠ Cₜ(vₜ) ∀vₛ,vₜ |
-
In the case of an empty input space
equiv(∅, Cₛ, Cₜ) := Yes and that is trivial to prove because there is no pair of values (vₛ, vₜ) that could be tested against the decision trees. In the other subcases S is always non-empty.
-
When there are Failure nodes at both sides the result is Yes:
equiv(S, Failure, Failure) := Yes Given that ∀v, Failure(v) = Failure, the statement holds.
-
When we have a Leaf or a Failure at the left side:
equiv(S, Failure as Cₛ, Switch(a, (πᵢ → Cₜᵢ)i∈I)) := Forall(equiv( S∩a→π(kᵢ)), Cₛ, Cₜᵢ)i∈I) equiv(S, Leaf bbₛ as Cₛ, Switch(a, (πᵢ → Cₜᵢ)i∈I)) := Forall(equiv( S∩a→π(kᵢ)), Cₛ, Cₜᵢ)i∈I) Our algorithm either returns Yes for every sub-input space Sᵢ := S∩(a→π(kᵢ)) and subtree Cₜᵢ
equiv(Sᵢ, Cₛ, Cₜᵢ) = Yes ∀i or we have a counter example vₛ, vₜ for which
vₛ≃vₜ∈Sₖ ∧ cₛ(vₛ) ≠ Cₜₖ(vₜ) then because
vₜ∈(a→πₖ) → Cₜ(vₜ) = Cₜₖ(vₜ) , vₛ≃vₜ∈S ∧ Cₛ(vₛ)≠Cₜ(vₜ) we can say that
equiv(Sᵢ, Cₛ, Cₜᵢ) = No(vₛ, vₜ) for some minimal k∈I -
When we have a Switch on the right we define πfallback as the domain of values not covered but the union of the constructors kᵢ
πfallback = ¬\bigcuplimitsi∈Iπ(kᵢ) Our algorithm proceeds by trimming
equiv(S, Switch(a, (kᵢ → Cₛᵢ)i∈I, Csf), Cₜ) := Forall(equiv( S∩(a→π(kᵢ)i∈I), Cₛᵢ, Ct/a→π(kᵢ))i∈I +equiv(S∩(a→πₙ), Cₛ, C_{a→πfallback}))The statement still holds and we show this by first analyzing the Yes case:
Forall(equiv( S∩(a→π(kᵢ)i∈I), Cₛᵢ, Ct/a→π(kᵢ))i∈I = Yes The constructor k is either included in the set of constructors kᵢ:
k | k∈(kᵢ)ⁱ ∧ Cₛ(vₛ) = Cₛᵢ(vₛ) We also know that
(1) Cₛᵢ(vₛ) = Ct/a→πᵢ(vₜ) (2) CT/a→πᵢ(vₜ) = Cₜ(vₜ) (1) is true by induction and (2) is a consequence of the trimming lemma. Putting everything together:
Cₛ(vₛ) = Cₛᵢ(vₛ) = CT/a→πᵢ(vₜ) = Cₜ(vₜ) When the k∉(kᵢ)ⁱ [TODO]
The auxiliary Forall function returns No(vₛ, vₜ) when, for a minimum k,
equiv(Sₖ, Cₛₖ, CT/a→πₖ = No(vₛ, vₜ) Then we can say that
Cₛₖ(vₛ) ≠ Ct/a→πₖ(vₜ) that is enough for proving that
Cₛₖ(vₛ) ≠ (Ct/a→πₖ(vₜ) = Cₜ(vₜ))