Francesco Mecca 5ea1311075 invio donatelli

2020-05-22 12:48:27 +02:00

33 KiB

Raw Blame History

Esercizio di analisi degli algoritmi di mutua esclusione

\begin{comment} NOTA: nel caso di Ampararore, la formula: | AG(EF(critical_P == 1)) | da qualsiasi stato e` sempre possibile arrivare a critical_P == 1 \end{comment}

Proprieta` del modello

Ogni modello successivamente mostrato rispetta le seguenti proprieta`: siano p e q due generici processi,

Mutua esclusione: garantisce che al piu` un solo processo e` nella sezione critica ad ogni istante. E` una proprieta` di safety.

G (¬cₚ∨¬c_q)
Assenza di deadlock: ogni qualvolta un processo e` in attesa di entrare nella sezione critica, eventualmente verra` concesso ad un processo di entrare nella sezione critica. E` una proprieta` di liveness.

G((wₚ∨w_q) → F(cₚ∨c_q))
Assenza di starvation individuale: ogni qualvolta un processo e` in attesa di entrare nella sezione critica, eventualmente gli verra` concesso.

G(wₚ → Fcₚ)

Rispetto all'assenza di deadlock, e` una proprieta` di liveness ancora piu` forte della precedente.

∀p, G(wₚ → Fcₚ)

Possiamo convertire queste tre formule LTL in formule equivalenti CTL anteponendo l'operatore di stato A:

AG (¬cₚ∨¬c_q)

AG(wₚ → AF(cₚ∨c_q)

AG(wₚ → AFcₚ)

Benche` non tutte le formule LTL possono essere convertite in una formula CTL equivalente anteponendo ad ogni operatore temporale l'operatore di stato A, per queste tre proprieta` possiamo.

Si specifica che i processi non sono forzati a progredire al di fuori della regione critica (possono rimanere per un tempo indeterminato nella sezione azione locale lₚ) e quindi:

G((wₚ∨w_q) → F(cₚ∨c_q) = false → G((lₚ∨l_q) → F(cₚ∨c_q)

G((lₚ∨l_q) → F(cₚ∨c_q) = true → G((wₚ∨w_q) → F(cₚ∨c_q)

Algoritmo 3.2

Due processi iterano all'infinito seguendo questo pseudocodice

while true:
      non-critical section
      await turn = ID
      critical section
      turn <- (ID%2)+1

NuSMV

Si e` deciso di modellare l'algoritmo usando per ognuno dei due processi un'enumerazione di 4 stati ed una variabile turno di tipo intero.

state: {begin, wait, critical, done};

\hrulefill \lstinputlisting[breaklines]{3.2.b.smv} \hrulefill

GreatSPN

Il codice utilizzato per le proprieta` CTL e` il seguente:

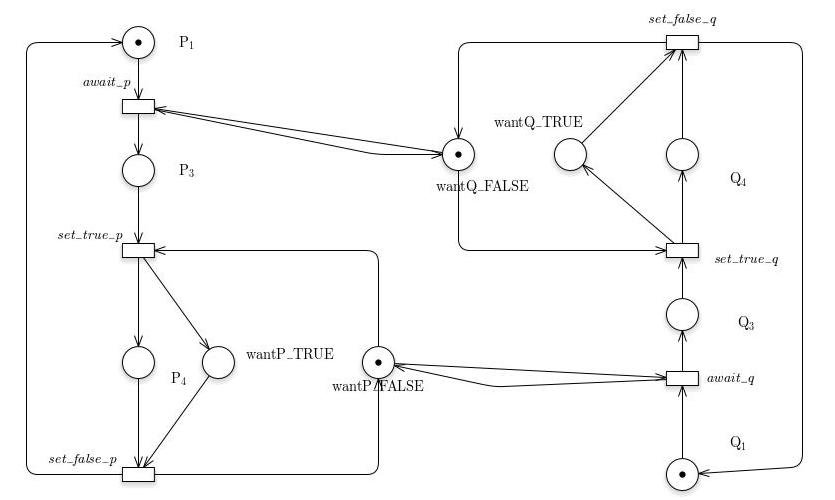
AG(!(#P3 == 1) || !(#P4 == 1))
AG ((#P1==1 || #Q1 == 1) -> AF (#P3 == 1 || #Q3 == 1))
AG (#P1==1 -> AF (#P3 == 1))
AG (#Q1==1 -> AF (#Q3 == 1))
AG (#Q1==1 -> EF (#Q3 == 1))

∈cludepdf{3.2.jpg}

Rete 3.2

Algebra dei processi

Riportiamo il modello dell'algoritmo 3.2 secondo l'algebra dei processi CSP.

System = {(P₁ || Q₁) || Tₚ} \ttvar{/ }Sync

Act = {localₚ, local_q, criticalₚ, critical_q}

Sync = {isₚ, is_q, setₚ, set_q}

Tₚ ::= isₚ.Tₚ + setₚ.Tₚ + set_q.T_q

T_q ::= is_q.T_q + setₚ.Tₚ + set_q.T_q

P₁ ::= localₚ.P₂ + localₚ.P₁

P₂ ::= isₚ.P₃

P₃ ::= criticalₚ.P₄

P₄ ::= set_q.P₁

Q₁ ::= local_q.Q₂ + local_q.Q₁

Q₂ ::= is_q.Q₃

Q₃ ::= critical_q.Q₄

Q₄ ::= set_p.Q₁

Seguono il Reachability Graph costruito con GreatSPN e il Derivation Graph.

∈cludepdf{rg_3.2.jpg}

Reachability Graph 3.2

∈cludepdf{derivation_3.2.jpg}

Derivation Graph 3.2

Risultati

Nella tabella mostriamo i risultati ottenuti

	NuSMV	GreatSPN
Mutua Esclusione	True	True
Assenza di deadlock	False	False
No Starvation	False	False

Il risultato della possibilita` di deadlock non deve stupire: la specifica non obbliga un processo a terminare la fase begin. Ne segue che anche l'assenza di starvation individuale non e` garantita. NuSMV conferma quanto detto mostrandoci un trace che fa da controesempio alla formula CTL:

\hrulefill

-- specification 
      AG (p.state = wait -> AF (p.state = critical | q.state = critical))  is false
-- as demonstrated by the following execution sequence
Trace Description: CTL Counterexample 
Trace Type: Counterexample 
  -> State: 1.1 <-
    turn = 1
    p.state = begin
    q.state = begin
  -> Input: 1.2 <-
    _process_selector_ = p
    running = FALSE
    q.running = FALSE
    p.running = TRUE
  -> State: 1.2 <-
    p.state = wait
  -> Input: 1.3 <-
  -> State: 1.3 <-
    p.state = critical
  -> Input: 1.4 <-
  -> State: 1.4 <-
    p.state = done
  -> Input: 1.5 <-
  -> State: 1.5 <-
    turn = 2
    p.state = begin
  -> Input: 1.6 <-
  -- Loop starts here
  -> State: 1.6 <-
    p.state = wait
  -> Input: 1.7 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -- Loop starts here
  -> State: 1.7 <-
  -> Input: 1.8 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -- Loop starts here
  -> State: 1.8 <-
  -> Input: 1.9 <-
    _process_selector_ = main
    running = TRUE
    p.running = FALSE
  -> State: 1.9 <-

\hrulefill \clearpage La traccia mostra che il processo q rimane nella fase begin e p, dopo essere entrato nella regione critica una volta, rimane bloccato in begin. Lo stesso trace mostra la possibilita` di starvation del processo. La rete modellata con GreatSPN ci conferma quanto visto con NuSMV. Inoltre il trace di GreatSPN ci mostra che non potendo forzare la fairness del modello, i processi possono iterare indefinitamente nella transizione iniziale, impedendo quindi il progresso dell'altro processo.

\hrulefill

Initial state is: P1(1), Turn_P(1), Q1(1)
Initial state satisfies: E F (not ((not (Q1 = 1)) or (not E G (not (Q3 = 1))))). 

1: P1(1), Turn_P(1), Q1(1)
  State 1. does not satisfy: ((not (Q1 = 1)) or (not E G (not (Q3 = 1)))). 

  1.1: P1(1), Turn_P(1), Q1(1)
    State 1.1.L. satisfies: (Q1 = 1). 

    State 1.1.R. satisfies: E G (not (Q3 = 1)). Start of loop.

    1.1.R.1: P1(1), Turn_P(1), Q1(1)
      State 1.1.R.1. does not satisfy: (Q3 = 1). 

    1.1.R.2: loop back to state 1.1.R.1.

\hrulefill \clearpage Prendiamo in considerazione la seguente formula CTL

AG (wₚ -> EF cₚ)

Sia GreatSPN che NuSMV ci mostrano che il sistema modellato rispetta questa proprieta`. Questo significa che un processo in attesa di entrare nella sezione critica ha la possibilita` di compiere progresso, ma solo nel caso in cui, come si intuisce dal controesempio precedente, l'altro processo decida di entrare in attesa a sua volta.

Algoritmo 3.5

Due processi iterano all'infinito seguendo questo pseudocodice

while true:
   await turn = ID
   turn <- (ID%2)+1

NuSMV

Si e` deciso di modellare l'algoritmo usando per ognuno dei due processi un'enumerazione di due stati e un contatore di turni intero

state: {await, done};

Non si e` utilizzata la direttiva process di NuSMV dato che un automa a stati finiti e` sufficiente a dimostrare le proprieta` del modello.

\hrulefill \lstinputlisting[breaklines]{3.5.smv} \hrulefill \clearpage

GreatSPN

Il codice utilizzato per le proprieta` CTL e` il seguente:

AG(!(#Await_P == 1) || !(#Await_Q == 1)) = true
AG ((#Wait_P==1 || #Await_Q == 1) -> AF (#Done_P == 1 || #Done_Q == 1)) = false
AG (#Await_P==1 -> AF (#Done_P == 1)) = false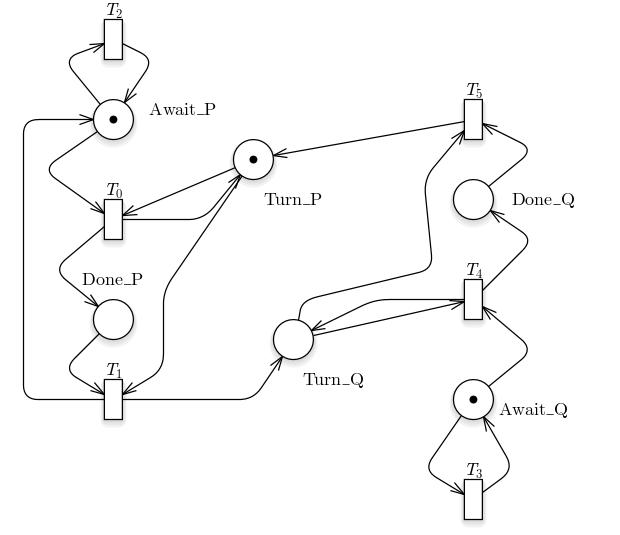

/bparodi/UniTO/media/commit/f317ed7c6b218cfb28cb6c777162fc4c9dc9d392/anno3/vpc/consegne/3/3.5.jpg — Rete 3.5

Risultati

Nella tabella mostriamo i risultati ottenuti

	NuSMV	GreatSPN
Mutua Esclusione	true	true
Assenza di deadlock	false	false
No Starvation	false	false

I risultati confermano il fatto che questo algoritmo e` solamente una versione semplificata del precedente (begin e wait sono stati fusi in await e done rimosso) e pertanto il trace di controesempio fornito da NuSMV e da GreatSPN presentano riflettono i risultati di questa semplificazione.

Possibilita` di deadlock:

  – specification AG ((p.state = await | q.state = await) -> AF (p.state = done | q.state = done))  is false
  – as demonstrated by the following execution sequence
  Trace Description: CTL Counterexample 
  Trace Type: Counterexample 
  – Loop starts here
  -> State: 1.1 <-
      turn = 1
      p.state = await
      q.state = await
  -> State: 1.2 <-

Possibilita` di starvation: i processi non compiono progresso iterando infinite volte su await.

  – specification AG (p.state = await -> AF p.state = done)  is false
  – as demonstrated by the following execution sequence
  Trace Description: CTL Counterexample 
  Trace Type: Counterexample 
  – Loop starts here
  -> State: 2.1 <-
      turn = 1
      p.state = await
      q.state = await
  -> State: 2.2 <-

  – specification AG (q.state = await -> AF q.state = done)  is false
  – as demonstrated by the following execution sequence
  Trace Description: CTL Counterexample 
  Trace Type: Counterexample 
  – Loop starts here
  -> State: 3.1 <-
      turn = 1
      p.state = await
      q.state = await
  -> State: 3.2 <-

Possibilita` di compiere progresso:

  specification AG (q.state = await -> EF q.state = done)  is true

Algoritmo 3.6

Due processi iterano all'infinito seguendo questo pseudocodice

while true:
    non-critical section
    await wantQ = false
    wantP <- true
    critical section
    wantP <- false

NuSMV

Si e` deciso di modellare l'algoritmo usando per ognuno dei due processi usando 5 stati

state: {local, await, critical, setTrue, setFalse};

\hrulefill \lstinputlisting[breaklines]{3.6.b.smv} \hrulefill \clearpage

GreatSPN

Il codice utilizzato per le proprieta` CTL e` il seguente:

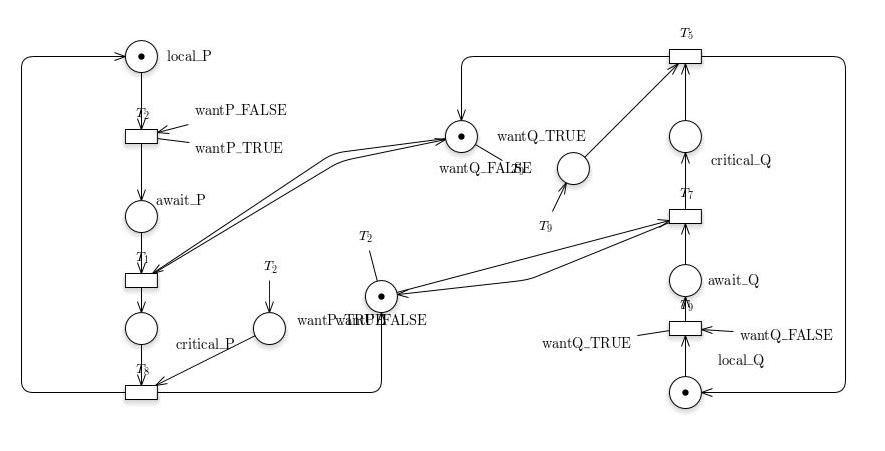
AG (!(#P4 == 1) || !(#Q4 == 1)) 
AG ((#P2==1 || #Q2 == 1) -> AF (#P4 == 1 || #Q4 == 1)) 
AG (#P1 == 1 -> EF(#Q4==1 || #Q4 == 1))
AG (#P2 == 1 -> AF (#P4 == 1))
AG (#Q2 == 1 -> AF (#Q4 == 1))

∈cludepdf{3.6.jpg}

Rete 3.6

Algebra dei processi

L'algoritmo 3.6 modellato secondo NuSMV e GreatSPN mostra che non c'e` la mutua esclusione. Questo viene evidenziato anche dal fatto che i nodi del Reachability Graph corrispondo al prodotto cartesiano P×Q. Anche il Derivation Graph del modello in algebra dei processi ha 25 nodi ed e` equivalente al Reachability Graph.

System = {(P₁ || Q₁) || (Wantₚ₀ || Want_q₀)} \ttvar{/ }Sync

Sync = { isTrueₚ, isFalseₚ, setTrueₚ, setFalseₚ,

ace{}\quad{}\quad{} isTrue_q, isFalse_q, setTrue_q, setFalse_q }

S = {localₚ, criticalₚ, local_q, critical_q}

Wantₚ₁ ::= isTrueₚ.Wantₚ₁ + setTrueₚ.Wantₚ₁ + setFalseₚ.Wantₚ₀

Wantₚ₀ ::= isFalseₚ.Wantₚ₀ + setFalseₚ.Wantₚ₀ + setTrueₚ.Wantₚ₁

P₁ ::= localₚ.P₁ + localₚ.P₂

P₂ ::= isFalse_q.P₃

P₃ ::= setTrueₚ.P₄

P₄ ::= criticalₚ.P₅

P₅ ::= setFalseₚ.P₁

Want_q₁ ::= isTrue_q.Want_q₁ + setTrue_q.Want_q₁ + setFalse_q.Want_q₀

Want_q₀ ::= isFalse_q.Want_q₀ + setFalse_q.Want_q₀ + setTrue_q.Want_q₁

Q₁ ::= local_q.Q₁ + local_q.Q₂

Q₂ ::= isFalse_p.Q₃

Q₃ ::= setTrue_q.Q₄

Q₄ ::= critical_q.Q₅

Q₅ ::= setFalse_q.Q₁

Seguono il Reachability Graph costruito con GreatSPN e il Derivation Graph.

∈cludepdf{rg_3.6.jpg}

Reachability Graph 3.6

∈cludepdf{derivation_3.6.jpg}

Derivation Graph 3.6

Risultati

Nella tabella mostriamo i risultati ottenuti

	NuSMV	GreatSPN
Mutua Esclusione	false	false
Assenza di deadlock	true	false
No Starvation	false	false

Il trace di NuSMV mostra che la mutua esclusione puo` non essere rispettata dato che le due variabili wantP e wantQ possono essere contemporaneamente false.

\hrulefill

-- specification AG (p.state != critical | q.state != critical)  is false
-- as demonstrated by the following execution sequence
Trace Description: CTL Counterexample 
Trace Type: Counterexample 
  -> State: 1.1 <-
    wantP = FALSE
    wantQ = FALSE
    p.state = local
    q.state = local
  -> Input: 1.2 <-
    _process_selector_ = p
    running = FALSE
    q.running = FALSE
    p.running = TRUE
  -> State: 1.2 <-
    p.state = await
  -> Input: 1.3 <-
  -> State: 1.3 <-
    p.state = setTrue
  -> Input: 1.4 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 1.4 <-
    q.state = await
  -> Input: 1.5 <-
  -> State: 1.5 <-
    q.state = setTrue
  -> Input: 1.6 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 1.6 <-
    wantP = TRUE
    p.state = critical
  -> Input: 1.7 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 1.7 <-
    wantQ = TRUE
    q.state = critical

\hrulefill \clearpage L'incoerenza del risultato dell'assenza di deadlock e` spiegabile dal fatto che nel caso di NuSMV non e` possibile che un processo rimanga nel primo stato (local) per un tempo indefinito mentre nel caso di GreatSPN e` possibile che il processo P vada nello spazio await e il processo Q decida di rimanere nel loop local_Q all'infinito. Notiamo che se forziamo i processi a fare del progresso dallo stato local, allora la formula CTL

AG(wₚ → AF(cₚ∨c_q)

risulta rispettata. Ancora meglio, piuttosto che rimuovere una transizione possibile, possiamo restringere la verifica dell'assenza di deadlock alla seguente formula CTL

AG (wₚ → EF (cₚ || c_q))

AG(#await_P\space== 1 -> EF(#critical_Q==1 || #critical_P == 1))

che risulta rispettata. L'assenza di starvation individuale non e` rispettata ne` in NuSmv ne` in GreatSPN in quanto e` possibile che uno dei due processi continui ad accedere alla sezione critica senza permettere all’altro di fare lo stesso.

\hrulefill

-- specification AG (q.state = await -> AF q.state = critical)  is false
-- as demonstrated by the following execution sequence
Trace Description: CTL Counterexample 
Trace Type: Counterexample 
  -> State: 3.1 <-
    wantP = FALSE
    wantQ = FALSE
    p.state = local
    q.state = local
  -> Input: 3.2 <-
    _process_selector_ = q
    running = FALSE
    q.running = TRUE
    p.running = FALSE
  -- Loop starts here
  -> State: 3.2 <-
    q.state = await
  -> Input: 3.3 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 3.3 <-
    p.state = await
  -> Input: 3.4 <-
  -> State: 3.4 <-
    p.state = setTrue
  -> Input: 3.5 <-
  -> State: 3.5 <-
    wantP = TRUE
    p.state = critical
  -> Input: 3.6 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 3.6 <-
  -> Input: 3.7 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 3.7 <-
    p.state = setFalse
  -> Input: 3.8 <-
  -> State: 3.8 <-
    wantP = FALSE
    p.state = local

\hrulefill \clearpage

Algoritmo 3.8

Due processi iterano all'infinito seguendo questo pseudocodice

while true:
    non-critical section
    wantP <- true
    await wantQ = false
    critical section
    wantP <- false

NuSMV

Si e` deciso di modellare l'algoritmo allo stesso modo del precedente.

\hrulefill \lstinputlisting[breaklines]{3.8.smv} \hrulefill \clearpage

GreatSPN

Il codice utilizzato per le proprieta` CTL e` il seguente:

AG(!(#critical_P == 1) || !(#critical_Q == 1)) 
AG ((#await_P==1 || #await_Q == 1) -> AF (#critical_P == 1 || #critical_Q == 1)) 
AG (#await_P==1 -> AF (#critical_P == 1))
AG (#await_Q==1 -> AF (#critical_Q == 1))

Inoltre, per confermare alcune ipotesi, si e` testata anche la seguente formula CTL:

AG(#await_P == 1 -> EF(#critical_Q==1 \vert{}\vert{} #critical_P == 1))

che conferma la presenza di deadlock causata dalle due variabili booleane.

/bparodi/UniTO/media/commit/f317ed7c6b218cfb28cb6c777162fc4c9dc9d392/anno3/vpc/consegne/3/3.8.jpg — Rete 3.8

Risultati

Nella tabella mostriamo i risultati ottenuti

	NuSMV	GreatSPN
Mutua Esclusione	True	True
Assenza di deadlock	False	False
No Starvation	False	False

Questo algoritmo rispetto al precedente garantisce la mutua esclusione, ma non ci permette di evitare il deadlock (e di conseguenza neanche la starvation individuale).

Di seguito riportiamo la traccia di NuSMV che mostra che il deadlock avviene quando i progetti eseguono setTrue nello stesso momento.

\hrulefill

-- specification AG ((p.state = await | q.state = await) -> AF (p.state = critical | q.state = critical))  is false
-- as demonstrated by the following execution sequence
Trace Description: CTL Counterexample 
Trace Type: Counterexample 
  -> State: 1.1 <-
    wantP = FALSE
    wantQ = FALSE
    p.state = local
    q.state = local
  -> Input: 1.2 <-
    _process_selector_ = p
    running = FALSE
    q.running = FALSE
    p.running = TRUE
  -> State: 1.2 <-
    p.state = setTrue
  -> Input: 1.3 <-
  -> State: 1.3 <-
    wantP = TRUE
    p.state = await
  -> Input: 1.4 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 1.4 <-
    q.state = setTrue
  -> Input: 1.5 <-
  -- Loop starts here
  -> State: 1.5 <-
    wantQ = TRUE
    q.state = await
  -> Input: 1.6 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -- Loop starts here
  -> State: 1.6 <-
  -> Input: 1.7 <-
    _process_selector_ = main
    running = TRUE
    p.running = FALSE
  -- Loop starts here
  -> State: 1.7 <-
  -> Input: 1.8 <-
    _process_selector_ = q
    running = FALSE
    q.running = TRUE
  -- Loop starts here
  -> State: 1.8 <-
  -> Input: 1.9 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -- Loop starts here
  -> State: 1.9 <-
  -> Input: 1.10 <-
    _process_selector_ = main
    running = TRUE
    p.running = FALSE
  -> State: 1.10 <-

\hrulefill \clearpage Mostriamo invece il controesempio generato da GreatSPN che ci mostra una condizione di starvation individuale, dove, come in precedenza, il processo Q rimane in local_Q.

\hrulefill

Generated counter-example: 
==================================== Trace ====================================
Initial state is: local_P(1), wantP_FALSE(1), wantQ_FALSE(1), local_Q(1)
Initial state satisfies:
  E F (not ((not (await_P = 1)) or (not E G (not (critical_P = 1))))). 

1: local_P(1), wantP_FALSE(1), wantQ_FALSE(1), local_Q(1)
  State 1. satisfies: ((not (await_P = 1)) or (not E G (not (critical_P = 1)))). 

  1.1: local_P(1), wantP_FALSE(1), wantQ_FALSE(1), local_Q(1)
    State 1.1. does not satisfy: (await_P = 1). 

2: SetTrue_P(1), wantP_FALSE(1), wantQ_FALSE(1), local_Q(1)
  State 2. satisfies: ((not (await_P = 1)) or (not E G (not (critical_P = 1)))). 

  2.1: SetTrue_P(1), wantP_FALSE(1), wantQ_FALSE(1), local_Q(1)
    State 2.1. does not satisfy: (await_P = 1). 

3: wantP_TRUE(1), await_P(1), wantQ_FALSE(1), local_Q(1)
  State 3. does not satisfy: ((not (await_P = 1)) or (not E G (not (critical_P = 1)))). 

  3.1: wantP_TRUE(1), await_P(1), wantQ_FALSE(1), local_Q(1)
    State 3.1.L. satisfies: (await_P = 1). 

    State 3.1.R. satisfies: E G (not (critical_P = 1)). Start of loop.

    3.1.R.1: wantP_TRUE(1), await_P(1), wantQ_FALSE(1), local_Q(1)
      State 3.1.R.1. does not satisfy: (critical_P = 1). 

    3.1.R.2: loop back to state 3.1.R.1.

\hrulefill \clearpage

Algoritmo 3.9

Due processi iterano all'infinito seguendo questo pseudocodice

while true:
    non-critical section
    wantP <- true
    while wantQ
        wantP <- false
        wantP <- true
    critical section
    wantP <- false

(l'altro processo segue uno pseudocodice simmetrico)

NuSMV

Si e` deciso di modellare l'algoritmo usando per ognuno dei due processi utilizzando l'espressione process per simulare di NuSMV e per ciascun process una variabile state di tipo enumerazione

state: {local, critical, setTrue, setFalse, resetTrue, resetFalse};

Benche` non fosse necessario distinguere il set della variabile booleana wantP, si e` preferito farlo in quanto l'enumerazione di tutti gli stati possibili, come evidenziato dal codice che segue, non risulta complesso.

\hrulefill \lstinputlisting[breaklines]{3.9.smv} \hrulefill \clearpage

GreatSPN

Il codice utilizzato per le proprieta` CTL e` il seguente:

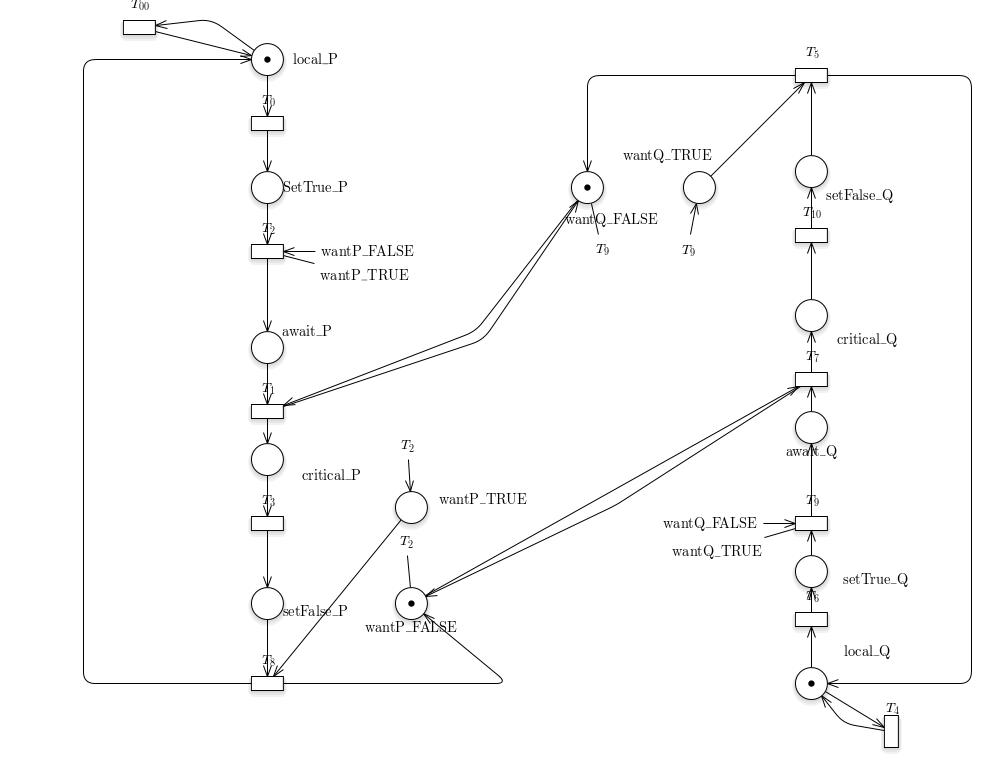
AG(!(#critical_P == 1) || !(#critical_Q == 1)) 
AG ((#setTrue_P==1 || #setTrue_Q == 1) -> AF (#critical_P == 1 || #critical_Q == 1)) 
AG (#setTrue_P==1 -> AF (#critical_P == 1))
AG (#setTrue_Q==1 -> AF (#critical_Q == 1))

Inoltre, per confermare alcune ipotesi, si e` testata anche la seguente formula CTL:

AG(#setTrue_P == 1 -> EF(#critical_Q==1

#critical_P == 1))

che conferma la presenza di deadlock causata dalle due variabili booleane.

∈cludepdf{3.9.jpg}

Rete 3.9

Risultati

Nella tabella mostriamo i risultati ottenuti

	NuSMV	GreatSPN
Mutua Esclusione	true	true
Assenza di deadlock	false	false
No Starvation	false	false

Il deadlock si verifica quando i entrambe le variabili booleane sono uguali a true. Ad esempio, se si esegue in locksetop il loop con la condizione booleana sulla variabile dell'altro processo, si verifica la condizione di deadlock. Viene riportato il trace di NuSMV che conferma questa ipotesi. GreatSPN fallisce per mancanza di RAM sulla macchina usata ma e` facile riprodurre il deadlock manualmente. \hrulefill

-- specification AG ((p.state = setTrue | q.state = setTrue) -> AF (p.state = critical | q.state = critical))  is false
-- as demonstrated by the following execution sequence
Trace Description: CTL Counterexample 
Trace Type: Counterexample 
  -> State: 1.1 <-
    wantP = FALSE
    wantQ = FALSE
    p.state = local
    q.state = local
  -> Input: 1.2 <-
    _process_selector_ = p
    running = FALSE
    q.running = FALSE
    p.running = TRUE
  -> State: 1.2 <-
    p.state = setTrue
  -> Input: 1.3 <-
  -> State: 1.3 <-
    wantP = TRUE
    p.state = critical
  -> Input: 1.4 <-
  -> State: 1.4 <-
    p.state = setFalse
  -> Input: 1.5 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 1.5 <-
    q.state = setTrue
  -> Input: 1.6 <-
  -> State: 1.6 <-
    wantQ = TRUE
    q.state = resetFalse
  -> Input: 1.7 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 1.7 <-
    wantP = FALSE
    p.state = local
  -> Input: 1.8 <-
  -> State: 1.8 <-
    p.state = setTrue
  -> Input: 1.9 <-
  -- Loop starts here
  -> State: 1.9 <-
    wantP = TRUE
    p.state = resetFalse
  -> Input: 1.10 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 1.10 <-
    wantQ = FALSE
    q.state = resetTrue
  -> Input: 1.11 <-
  -- Loop starts here
  -> State: 1.11 <-
    wantQ = TRUE
    q.state = resetFalse
  -> Input: 1.12 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 1.12 <-
    wantP = FALSE
    p.state = resetTrue
  -> Input: 1.13 <-
  -- Loop starts here
  -> State: 1.13 <-
    wantP = TRUE
    p.state = resetFalse
  -> Input: 1.14 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 1.14 <-
    wantQ = FALSE
    q.state = resetTrue
  -> Input: 1.15 <-
  -- Loop starts here
  -> State: 1.15 <-
    wantQ = TRUE
    q.state = resetFalse
  -> Input: 1.16 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 1.16 <-
    wantP = FALSE
    p.state = resetTrue
  -> Input: 1.17 <-
  -> State: 1.17 <-
    wantP = TRUE
    p.state = resetFalse

\hrulefill \clearpage Di seguito il trace che conferma la presenza di starvation individuale, sia in GreatSPN che NuSMV.

\hrulefill

Generated counter-example: 
==================================== Trace ====================================
Initial state is: local_Q(1), wantQ_FALSE(1), wantP_FALSE(1), local_P(1)
Initial state satisfies:
  E F (not ((not (setTrue_Q = 1)) or (not E G (not (critical_Q = 1))))). 

1: local_Q(1), wantQ_FALSE(1), wantP_FALSE(1), local_P(1)
  State 1. satisfies: ((not (setTrue_Q = 1)) or (not E G (not (critical_Q = 1)))). 

  1.1: local_Q(1), wantQ_FALSE(1), wantP_FALSE(1), local_P(1)
    State 1.1. does not satisfy: (setTrue_Q = 1). 

2: setTrue_Q(1), wantQ_FALSE(1), wantP_FALSE(1), local_P(1)
  State 2. does not satisfy: ((not (setTrue_Q = 1)) or (not E G (not (critical_Q = 1)))). 

  2.1: setTrue_Q(1), wantQ_FALSE(1), wantP_FALSE(1), local_P(1)
    State 2.1.L. satisfies: (setTrue_Q = 1). 

    State 2.1.R. satisfies: E G (not (critical_Q = 1)). Start of loop.

    2.1.R.1: setTrue_Q(1), wantQ_FALSE(1), wantP_FALSE(1), local_P(1)
      State 2.1.R.1. does not satisfy: (critical_Q = 1). 

    2.1.R.2: loop back to state 2.1.R.1.

\hrulefill \clearpage \hrulefill

-- specification AG (q.state = setTrue -> AF q.state = critical)  is false
-- as demonstrated by the following execution sequence
Trace Description: CTL Counterexample 
Trace Type: Counterexample 
  -> State: 3.1 <-
    wantP = FALSE
    wantQ = FALSE
    p.state = local
    q.state = local
  -> Input: 3.2 <-
    _process_selector_ = q
    running = FALSE
    q.running = TRUE
    p.running = FALSE
  -> State: 3.2 <-
    q.state = setTrue
  -> Input: 3.3 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 3.3 <-
    p.state = setTrue
  -> Input: 3.4 <-
  -> State: 3.4 <-
    wantP = TRUE
    p.state = critical
  -> Input: 3.5 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 3.5 <-
    wantQ = TRUE
    q.state = resetFalse
  -> Input: 3.6 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -- Loop starts here
  -> State: 3.6 <-
    p.state = setFalse
  -> Input: 3.7 <-
    _process_selector_ = main
    running = TRUE
    p.running = FALSE
  -- Loop starts here
  -> State: 3.7 <-
  -> Input: 3.8 <-
    _process_selector_ = q
    running = FALSE
    q.running = TRUE
  -> State: 3.8 <-
    wantQ = FALSE
    q.state = resetTrue
  -> Input: 3.9 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 3.9 <-
    wantP = FALSE
    p.state = local
  -> Input: 3.10 <-
  -> State: 3.10 <-
    p.state = setTrue
  -> Input: 3.11 <-
  -> State: 3.11 <-
    wantP = TRUE
    p.state = critical
  -> Input: 3.12 <-
    _process_selector_ = q
    q.running = TRUE
    p.running = FALSE
  -> State: 3.12 <-
    wantQ = TRUE
    q.state = resetFalse
  -> Input: 3.13 <-
    _process_selector_ = p
    q.running = FALSE
    p.running = TRUE
  -> State: 3.13 <-
    p.state = setFalse

\hrulefill \clearpage

Algoritmo di Dekker per la mutua esclusione

Due processi iterano all'infinito seguendo questo pseudocodice

while true:
    non-critical section
    wantP <- true
    while wantQ:
        if turn = 2:
            wantp <- false
            await turn = 1
            wantp <- true
    critical section
    turn <- 2
    wantp <- false

(l'altro processo segue uno pseudocodice simmetrico)

NuSMV

Si e` deciso di modellare l'algoritmo usando per ognuno dei due processi usando 9 stati

state: {local, set_true, while, loop_set_false, await, loop_set_true, critical, switch_turn, set_false};

\hrulefill \lstinputlisting[breaklines]{dekker_WN.smv} \hrulefill \clearpage

GreatSPN

Il codice utilizzato per le proprieta` CTL e` il seguente:

AG(!(#critical_P == 1) || !(#critical_Q == 1)) 
AG ((#local_P==1 || #local_Q == 1) -> AF (#critical_P == 1 || \#critical_Q == 1)) 
AG (#local_P==1 -> AF (#critical_P == 1))
AG (#local_Q==1 -> AF (#critical_Q == 1))

∈cludepdf{dekker.jpg} Ci aspettiamo che come in precedenza ci sia deadlock perche` viene data ai processi la possibilita` di rimanere su local. Forzando i processi a fare del progresso dallo stato local, allora la formula CTL

Rete 3.10

AG((lₚ || l_q) → AF(cₚ∨c_q)

risulta rispettata. Ancora meglio, piuttosto che rimuovere una transizione possibile, possiamo restringere la verifica dell'assenza di deadlock alla seguente formula CTL

AG (wₚ → EF (cₚ || c_q))

AG(#await_P\space== 1 -> EF(#critical_Q==1 || #critical_P == 1))

che risulta rispettata.

C'e` possibilita` di starvation individuale perche` a differenza di NuSMV non possiamo rispettare il requisito di fairness.

Risultati

Nella tabella sono mostrati i risultati ottenuti

	NuSMV	GreatSPN
Mutua Esclusione	true	true
Assenza di deadlock	true	false
No Starvation	true	false

Equivalenza in algebra dei processi

Precedentemente abbiamo modellato usando l'algebra dei processi l'algoritmo 3.2 e l'algoritmo 3.6. Entrambi hanno le seguenti azioni:

S = {localₚ, criticalₚ, local_q, critical_q} ∪ {τ}

Bisimulazione

Si applica l'algoritmo del partizionamento per verificare l'equivalenza tramite bisimulazione. Questo lo stato iniziale

{S0, R0}, {S1, S2, S3, S4, S5, S6, S7, S8, S9, S10, S11, S12, S14, S13

R1, R2, R2, R3, R4, R5, R6, R7, R8, R9, R10, R11, R12, R13, R14, R15,

R16, R17, R18, R19, R20, R21, R22, R23, R24}

Applico lo split considerando l'azione criticalₚ

{S0, R0}, {S4, S5, R4, R14, R18, R19, R24}

{S1, S2, S3, S6, S7, S8, S9, S10, S11, S12, S14, R1, R2, R3, R5, R6,

R7, R8, R9, R10, R11, R12, R13, R15, R16, R17, R20, R21, R22, R23}

Applico lo split considerando l'azione critical_q

{S0, R0}, {S4, S5, R4, R14, R19, R24}, {R18}, {S11, S13, R9, R11, R16, R22}

{S1, S2, S3, S6, S7, S8, S9, S10, S12, S14, R1, R2, R3, R5, R6,

R7, R8, R10, R12, R13, R15, R17, R20, R21, R23}

Notiamo che R18 compare come unico elemento di un insieme. Benche` l'algoritmo non sia terminato, questo ci basta per concludere che non c'e` bisimulazione fra i due algoritmi. Nell'algoritmo 3.2 non compare nessuno stato da cui e` possibile effettuare l'azione criticalₚ o l'azione critical_q. Questo risultato si poteva dedurre dal fatto che l'algoritmo 3.6 a differenza del 3.2 non rispetta la mutua esclusione e quindi vi sono degli stati non rappresentabili nel modello dell'algoritmo 3.2. Si noti che non e` strettamente necessario mascherare le azioni isₚ, is_/q, setₚ, set_/q/ in quanto presenti in entrambi i modelli. Nel caso di bisimulazione fra due modelli, l'algoritmo raggiunge la terminazione quando non e` piu` possibile partizionare gli insieme in base alle azioni comuni e abbiamo come risultato che in ogni set compare uno stato di un modello insieme ad uno o piu` stati dell'altro.

Trace equivalence

La trace equivalence e` piu` debole della bisimulation equivalence:

p ∼ q → p ⋍_T q

ma non viceversa

p ∼ q ↛ p ⋍_T q

Dato che l'algoritmo 3.6 non rispetta la mutua esclusione, possiamo affermare che una sequenza s dove criticalₚ e critical_q appaiono in successione, non e` una sequenza valida per il modello dell'algoritmo 3.2 ma lo e` per il modello dell'algoritmo 3.6.

s = …criticalₚcritical_q…

s = …critical_qcriticalₚ…

Questo ci permette di dire che non c'e` trace equivalence fra i due modelli.

Riduzione

Le reti dell'algoritmo 3.6 e 3.8 differiscono per la successione delle istruzioni di setTrue e await e permettono simmetricamente le stesse riduzioni:

rete 3.6	rete 3.8
rimozione self loop	rimozione self loop
fusione posti P1-P2	fusione posti local_P, setTrue_P
fusione posti P4-P5	fusione posti critical_P, setFalse_P
fusione posti Q1-Q2	fusione posti local_Q, setTrue_Q
fusione posti Q4-Q5	fusione posti critical_Q, setFalse_Q

Riportiamo le immagini delle due reti ridotte. Le transizioni relative a setTrue e await non sono riducibili in quanto hanno archi uscenti. Possiamo affermare che le due reti non sono equivalenti, come era deducibile dal fatto che rispettano diverse proprieta`.

/bparodi/UniTO/media/commit/f317ed7c6b218cfb28cb6c777162fc4c9dc9d392/anno3/vpc/consegne/3/ridotto_3.6.jpg — Riduzione rete 3.6

/bparodi/UniTO/media/commit/f317ed7c6b218cfb28cb6c777162fc4c9dc9d392/anno3/vpc/consegne/3/ridotto_3.8.jpg — Riduzione rete 3.8

33 KiB Raw Blame History Unescape Escape

Esercizio di analisi degli algoritmi di mutua esclusione

Proprieta` del modello

Algoritmo 3.2

NuSMV

GreatSPN

Algebra dei processi

Risultati

Algoritmo 3.5

NuSMV

GreatSPN

Risultati

Algoritmo 3.6

NuSMV

GreatSPN

Algebra dei processi

Risultati

Algoritmo 3.8

NuSMV

GreatSPN

Risultati

Algoritmo 3.9

NuSMV

GreatSPN

Risultati

Algoritmo di Dekker per la mutua esclusione

NuSMV

GreatSPN

Risultati

Equivalenza in algebra dei processi

Bisimulazione

Trace equivalence

Riduzione

33 KiB

Raw Blame History